PDF

Int J Med Sci 2007; 4(3):164-173. doi:10.7150/ijms.4.164 This issue Cite

Research Paper

Cancer control through principles of systems science, complexity, and chaos theory: A model

Ivo P. Janecka

Health Research International, 333 Westbrook Rd, St. Helena Island, SC 29920, USA

Abstract

Cancer is a significant medical and societal problem. This reality arises from the fact that an exponential and an unrestricted cellular growth destabilizes human body as a system. From this perspective, cancer is a manifestation of a system-in-failing.

A model of normal and abnormal cell cycle oscillations has been developed incorporating systems science, complexity, and chaos theories. Using this model, cancer expresses a failing subsystem and is characterized by a positive exponential growth taking place in the outer edge of chaos. The overall survival of human body as a system is threatened. This model suggests, however, that cancer's exponential cellular growth and disorganized complexity could be controlled through the process of induction of differentiation of cancer stem cells into cells of low and basic functionality.

This concept would imply reorientation of current treatment principles from cellular killing (cyto-toxic therapies) to cellular retraining (cyto-education).

Keywords: systems, complexity, chaos, cancer, melatonin, physical activity

1. Introduction

Motto: “The more we study the major problems of our time, the more we come to realize that they cannot be understood in isolation. They are systemic problems, which means that they are interconnected and interdependent.” Fritjof Capra [1].

Cancer is a significant biologic and social problem. Effective cancer control should be reflected in a progressive reduction in cancer mortality. This has not been achieved in the last 30 years of a focused war on cancer. Leaf [2] wrote that “since the crusade began with the [US]National Cancer Act in 1971, we are far from winning the war…it looks like [we are] losing….some $200 billion later, the five-year survival rate is 63%, a modest 13-point gain.” The purpose of this paper is to apply principles of systems science, complexity, and chaos theory to the unrestrained growth of malignant cells and explore ways how to regain control over them.

All living things experience various iterations of pendulum-like swings in their morphology and physiology which are controlled by resetting mechanisms. For each cycle there is a defined beginning and an end. Cycles do not exist in isolation as they are all part of a continuum, from small cycles to larger ones. Each cycle absorbs some characteristics of smaller cycles and provides components to larger ones as well. Cycles express relatedness, a key characteristic of systems, implying the interconnectedness and dependability of all components.

From stem cells to human beings, pendulum-like oscillations take place, ranging from a daily sleep-awake cycle to the ultimate birth-death cycle. These changes have an optimal zone of function. Outside of the range, the function morphs into dysfunction with increasing cycle instability leading to a great evolutionary uncertainty through mutations. Iterations of each cycle require a resetting mechanism which triggers a change in the trajectory of each imaginary pendulum. Such resetting is either inherent within the entity itself or is part of some external cycle.

This study hypothesizes a multi-level model in order to assist in understanding of complex systems with the ability to express dynamic states with transitions in and out of various boundaries. A single-level model would help to elucidate the function and structure of a component, a subsystem, but only the integration of all known levels provides a full system's view. Human body is a large system with a hierarchy of vast number of subsystems engaged in self-organization and self-adaptation.

Research questions:

1. Can systems science, complexity, and chaos theory be applied to cells and other biologic entities within a framework of a model?
2. Can such theories be helpful in understanding of normal and abnormal cellular growth including cancer?
3. Can such theories point to a therapeutic paradigm in cancer control?

2. Concepts

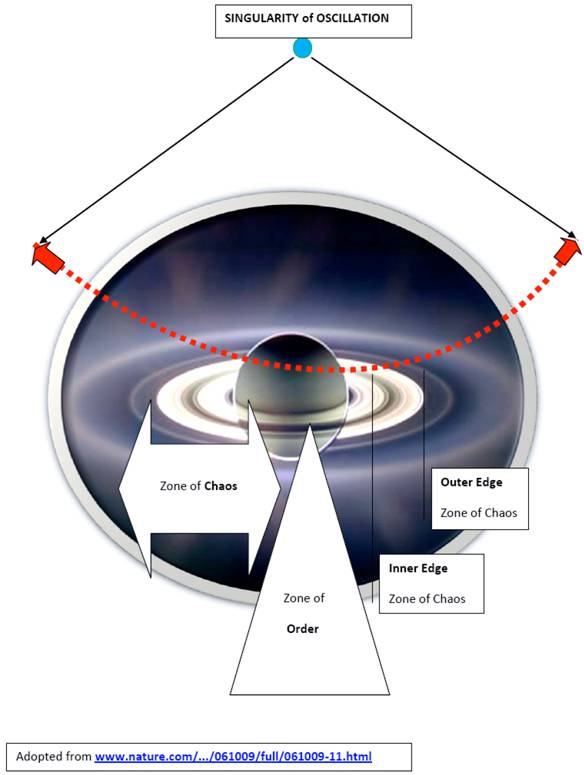
This model conceptualizes the existence of zones of order and chaos, with ongoing pendulum-like transitions of life entities through them, from the initial state to the end state (Fig. 1). A potential also exists for aberrant paths leading to cancer or degenerative/inflammatory diseases. The center of this model lies in the health territory, which is straddling the outer core of the zone of order and the inner edge of chaos (Fig. 2, 3). The health territory is an active space of self-organization and self-adaptation within a nonlinear dynamical system following the principles of organized complexity; stable boundaries depend on the efficacy of resetting mechanisms. Outside of the boundaries of a well-functioning system's health territory, a living entity can enter either further into the zone of chaos or a zone of entropy, each dramatically affecting the system. All terms expressing concepts of this model and systems, complexity, and chaos are italicized for emphasis.

 Figure 1 

This model conceptualizes the existence of zones of order and chaos, with ongoing pendulum-like transitions of life entities through them.

 Figure 2 

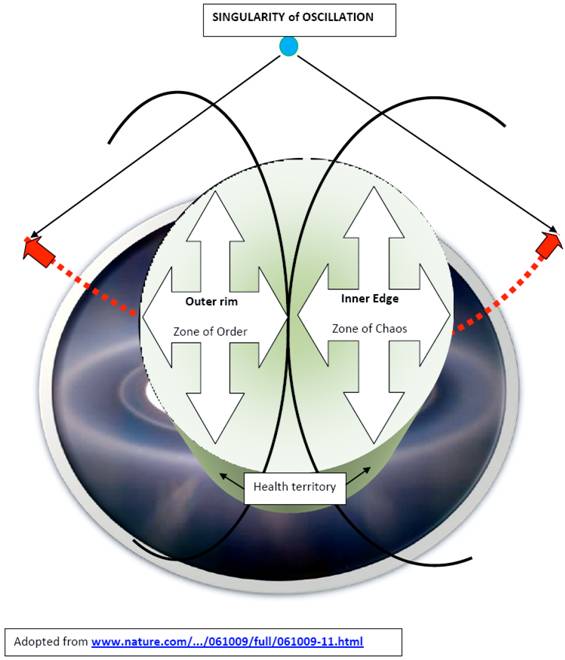
The center of this model lies in the health territory, which is straddling the outer core of the zone of order and the inner edge of chaos.

A singularity of oscillation is an imaginary fixed point of the pendulum-like movements. Embryonic stem cell renewals may serve as an example of such repetitious endless cycles of multiplication. A singularity of differentiation, on the other hand, is conceptualized as a different point of oscillations which is characterized by a pre-set number of cell cycle repetitions and by some specificity of functioning. Progenitor cells may serve as such an example.

The development of this model begins with an initial state. It is a pre-system phase because a true system does not exist yet; there are only potentialities among the multiple components for new relationships and the creation of a system's emergence. This state is characterized by randomness and in system's terminology-equipotentiality [3]. This state can advance to self-organization, a process going “…toward higher differentiation” [3]. In human evolution, this could be analogous to the movement of sperms prior to fertilization.

The systems' evolutionary phase follows the completion of the initial state but prior to a stage of a fully-functioning open system. It is epitomized by embryogenesis with the onset of complexity and self-organization during the development of the system's emergence, a new living entity. It is still a closed system which exists during a time-limited gestation; once enough complexity and self-organization is present, the closed system must become an open system which takes place during birth. In an open system, there is a proportionate gradient of energy and information between the intake and the output, creating system's functionality. Embryogenesis, systematized as the evolution of multiple subsystems into a large system, is characterized by an exponential growth, the presence of significant angiogenesis, and temporary protection from immunosurveilance of a larger open system (the mother), among other features. This process is pre-programmed to end when the closed system needs to change into an open system. If a successful transition doesn't take place, the closed system of embryogenesis and ontogenesis spirals into maximum entropy and ceases to exist (e.g. a stillbirth).

A fully functioning open system expresses a number of defining characteristics. Among the predominant features are: relationships, communication, self-organization and self-adaptation, and the potential to create a new emergence. System's stability depends on the quality and the quantity of patterned relationships and their interactions. In an open system, the balance is not just a reflection of its internal relationships (self-organization) but also its larger external relationships to larger systems (self-adaptation). System's resiliency is related to its redundancy.

 Figure 3 

Carcinogenesis in the zone of chaos.

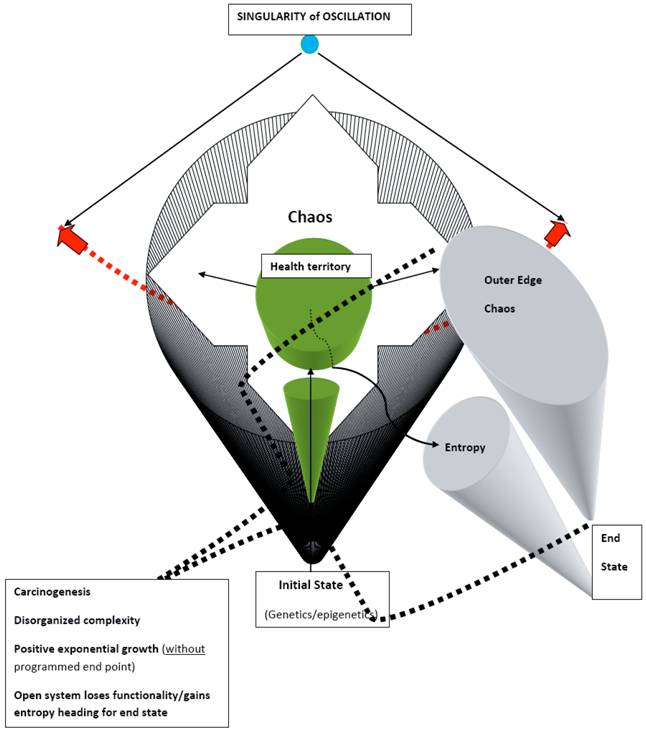
The system's attributes and relationships can be identified within a healthy human body which is an excellent example of a robust open system. By contrast, unhealthy human body exhibits inconsistent compliance with system's principles. Cancer, when seen from this system's perspective, initially exhibits features of a failing specific cellular subsystem with the potential to overwhelm the entire system by propagation of faulty DNA to RNA transcription. Degenerative and inflammatory diseases would follow a mirror path in this schema, not a path of positive exponential growth but a path of entropy with negative exponential growth. This is accompanied by the loss of a favorable gradient of energy and information, both essential to the functionality of an open system.

The overall cancer process can be conceptualized as a “system-in-failing,” from a localized cancer representing a subsystem failure, to a metastatic cancer that can be seen as a total large system failure heading for its termination. Cancer, known to express an exponential growth of cells, places this stage graphically in the outer edge of the zone of chaos of the model. At this point, the entire system's survival is being threatened. From this perspective, cancer cure would require not just successful cancer therapy of the gross disease, in order to limit the total cancer burden of the system, but also simultaneously understand and correct the “why” and “where” the entire biologic system went awry. Otherwise, the likelihood of developing another clinically apparent cancer is high.

Waldrop [4] describes chaos as a nonlinear phenomenon [where]…a tiny event over here can have an enormous effect over there…the flap of a butterfly's wings in Texas could change the course of a hurricane in Haiti a week later…everything is connected and often with incredible sensitivity. Tiny perturbations won't always remain tiny. Under the right circumstance [and critical timing], the slightest uncertainty can grow until the system's future becomes utterly unpredictable…chaotic…[a] pattern of ever-increasing [disorganized] complexity.

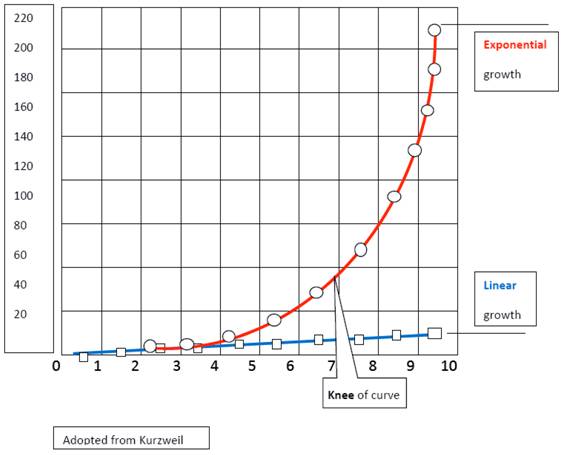
Chaos is characterized by exponential iterations with a potential for runaway growth acceleration. A graphic comparison of a positive exponential curve with a linear line can express the relationship between normal and malignant growth (Fig. 5). The inner edge of chaos approximates the shape of the initial segment of an exponential growth curve and runs in near proximity of a linear curve which represents a normal rhythmic growth. At the knee of the exponential curve, there is a significant divergence between longitudinal changes and the exponential ones; the outer edge of chaos begins here. The important ingredients of a functioning system, relationships, communications, and organized complexity are breaking down along this parabolic path and on a cellular level, the transcription of DNA to RNA is altered within the basic units of the subsystems, the stem cells. Kornberg [5] stated that “Disturbances in the transcription process are involved in many human illnesses such as cancer, heart disease and various kinds of inflammation…[and that] the capacity of stem cells to develop into different types of specific cells with well-defined functions in different organs, is also linked to how the transcription is regulated.” The structural and functional dilemmas of being in the zone of chaos have to be eventually resolved by living entities, either with the return to physiologic oscillation or by allowing the undifferentiated growth to continue into cancer formation [6].

The final evolutionary phase of a pendulum-like oscillating system in this model is the system's devolutionary phase, expressing degeneration, inflammation, and senescence. This phase also begins outside of the health territory and precedes the end state. It can be seen as a reverse mirror image of the system's evolutionary phase as the system loses its organized complexity, self-organization and self-adaptation, and looks less and less like an open system. Randomness and disorganized complexity with mutations have returned and functionality is decreasing due to increasing entropy; the whole system is closing down. Laszo [7] stated that “entropy can only increase in time in any isolated system [and that] such a system runs down [due to the fact that] the sum of the energies used up is always negative-more energy is used up than is generated.” The frequency of mutations is increasing in this phase with a potential shortcut from entropy to a positive exponential growth leading to cancer, connecting cancer and aging. Downregulation of sirtuins genes play an important role in this process [8].

The end state follows system's devolutionary phase at which point a system ceases to exist as an open system and begins to resemble a closed system with a minimum of energy and information exchange. Even randomness ends due to the overwhelming entropy; the system ends. “A closed system must…eventually attain a time-independent state of equilibrium, defined by maximum entropy and minimum free energy…” [3].

Human aging and degenerative/inflammatory diseases resemble the devolutionary phase. From system's perspective, aging, classically thought to parallel increasing frailty, involves a phase transition of life cycle into entropy which often manifests itself as degenerative/inflammatory diseases. There is also an increase in mutations which can connect this phase with the outer edge of chaos and the increase incidence of cancer. Dying reflects changes from an open into a closed system. An active enhancement of longevity correspondingly suppresses cancer development. The sirtuin genes have been identified experimentally as proteins associated with increasing life span. ” Goymer [9] stated that, “mutations that extend lifespan in Caenorhabditis elegans also inhibit tumour growth.”

Physiologic resetting is the guardian process of the health territory allowing oscillation within its boundaries. It is defined as a point of active interference with a given cycle trajectory as it approaches its climax of criticality. Either resetting of an old cycle around previous singularity takes place, or a new cycle, based at a singularity of differentiation, begins. Resetting is also a stimulus which propels a biologic entity from one zone to another. In its simple form, resetting may be considered a switch which can, however, turn into autocatalysis of either only positive or only negative feedback loop mechanism. The resetting impetus can be either internal and/or an external one. Examples may include: the light-melatonin-sleep/awake variations or gene activation of the cellular life/death cycle where multiple genes participate, such as RNA interference, p53 gene, RB gene, sirtuins, telomerase, etc.

Complexity governs the myriad of interactions within a system. “Complexity…[is] a science of emergence” [4] allowing system's ultimate mission, the creation of emergence. Complexity gradually evolves within the system's evolutionary phase, reaches its greatest functionality, the orderly complexity within the health territory, and then steadily declines during system's devolutionary phase expressing disorderly complexity. As Kurtzweil [10] said, “complexity is a continuum.” Where complexity is at any given time, within its continuum, depends on its functionality, which is a ration of the engaged complexity components vs. those that are not engaged in productive energy-generating and information-sharing interactions. Complexity expresses the functionality of a system and reflects the process of relationships which produces self-organization and self-adaptation. Complexity begins to appear at a distance from the initial state, when randomness gives way to self-organization. It is “…spontaneous emergence of order…[allowed by] a constant flow of energy and matter through the system…[the] emergence of new structures and new forms of behavior…[which are] the hallmark of self-organization, [and] occurs only when the system is far from equilibrium” [1]. Self-organization reflects the evolving interactions of innumerable relationships of the system's components. As the end-product of self-organization is system's emergence, the opposite state reflects instability, increase of errors/mutations, and a potential for total randomness. Kurtzweil [10] stated that, “a key requirement for a self-organizing system is a nonlinearity;” he also pointed out that “…a lot of nature is not linear….” “The self-organizing systems…[are] governed by nonlinear dynamics…” [4]. In contrast stands the traditional linear system “in which the whole is precisely equal to the sum of its parts…[and its] plot is a straight line…” [4].

 Figure 4 

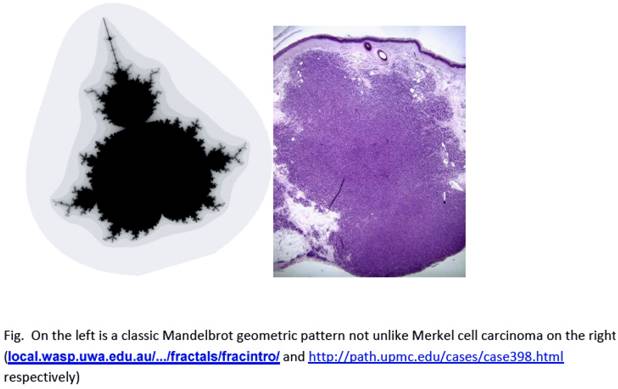
Similarity between Mandelbrot fractal pattern and cancer (Merkel cell carcinoma).

 Figure 5 

A comparison of a positive exponential curve with a linear one expresses the relationship between normal and malignant growth (Modified from Kurtzweil).

Complex adaptive systems (CAS) express a high degree of resilience and robustness to environmental challenges through their self-adaptation and internal self-organization. “They actively try to turn whatever happens to their advantage…a kind of dynamism that makes them qualitatively different from static objects such as computer chips or snowflakes, which are merely complicated” [4]. One important characteristic of CAS is that “…the control of a complex adaptive system tends to be highly dispersed” [4].

A modified image of the planet Saturn with its rings (Fig. 1) provides a visual expression of the presented model with a superimposed pendulum, oscillating from a point of singularity. The planet's rings represent the inner and the outer edges of chaos. The planet itself is imagined as the zone of order of this model with an inner and an outer core. The inner core represents a linear, rigid space in the model where the oscillating pendulum encounters friction which persistently tries to bring the pendulum to a halt. To continue its oscillation, pendulum needs ongoing inflow/outflow of energy and information involved in generating complexity. The basic level of complexity can be expressed here even in mechanistic terms, analogous to Newtonian physics, and allows for a linear prediction of future states with great degree of uniformity but it lacks adequate adaptability.

The detrimental rigidity of the inner core of the zone of order can be observed clinically when spontaneous fluctuations in the heart electrical signal are severely limited. Both Ludwig [11] and Goldberger et al [12] demonstrated the need for a degree of chaos in a healthy heart. An electrocardiogram without a degree of chaos actually reflects an underlying cardiac abnormality, especially the lack of adaptability. These observations support to view that a perfect order is a non-physiological and a non-healthy state. A degree of variability is essential to maintain a complex adaptive system. A biologic entity in this range is in danger of system failure from a sudden change as its prevailing rigid predictability has suppressed its functional adaptation.

The outer core of the zone of order engages in some functional adaptation; the system is responsive to changes within a certain range. When the outer core combines with the inner edge of chaos, it forms the health territory where system's components are routinely replaced but the basic relationships and methods of communication persist. In this healthy state, living entities are undergoing cellular renewals; immunosurveilance is functioning well, and agniogenesis has its limits.

The entire zone of chaos is expressed in fractals which is the architecture of multidimensional geometric patterns ubiquitous in nature. They express a feature of self-affinity and self-similarity at various scales (eg. branching of trees or a pattern of angiogenesis). “Fractal geometry…[is a] mathematical language to describe the fine-scale structure of chaotic attractors…[Authored by] the French mathematician Benoit Mandelbrot…to describe and analyze the complexity of the irregular shapes in the natural world…” [1]. The branching of a fractal pattern is related to the sudden appearance of a new chaotic attractor causing the bifurcation of an established pattern of growth.

All of these complex systems have somehow acquired the ability to bring order and chaos into a special kind of balance. This balance point…called the edge of chaos…where the components of a system never quite lock into place, and yet never quite dissolve into turbulence…where life has enough stability to sustain itself and enough creativity to deserve that name of life…where new ideas and innovative genotypes are forever nibbling away at the edge of the status quo… [1].

“The edge of chaos is the constantly shifting battle zone between stagnation and anarchy…place where a complex system can be spontaneous, adaptive, and alive” [4]. The similarity of a fractal pattern and cancer growth can be seen in a comparison of Mandelbrot's drawing and a histologic picture of Merkel cell carcinoma (Fig. 4).

The outer edge of chaos represents a far from equilibrium state where immunosurveilance is malfunctioning and neoagniogenesis has no limits. From here, cells may undergo exponential malignant growth or a cell death, apoptosis. In this region of the model, cells basically stop communicating with the entire system, breaking off system-wide relationships, and grow at the expense of the larger system; some feedback loops persist but only in order for tumor cells to harness the energy of the system. The transcription of DNA to RNA is altered.

There exist several options of progressions open to living entities such as cells which are within the health territory: cells can continue to divide as needed by the system (an example could be adult stem cells); cells can be programmed to undergo differentiation with a limited number of divisions (an example could be progenitor cells); cells can also undergo senescence with apoptosis. It is also possible that cells undergo an exponential malignant growth (cancer) if their original programming for a fixed number of cell divisions fails. Cancer develops within the outer edge of the zone of chaos where cells exhibit the exponential growth phase; when plotted, the growth pattern approximates the parabolic phase of a positive exponential curve beyond its knee. It is here that self-organizing and self-adapting relationships of the entire system are visibly weakened making cancer a product of a failing system; the neoangiogenesis is activated and immunosurvailance fades. Malignant cells may also appear within the inner edge of chaos but their growth follows only the first segment of the exponential curve which approximates the longitudinal line. The integrity of the system is still intact and neoangiogenesis has not been activated yet; immunosurvailance is still active.

On a cellular level, this model exemplifies the processes of adult stem cells. Tan et al [13] summarized that,

Normal adult stem cells are tissue-specific…[with] the ability to self-renew and to differentiate…[they] can undergo an unlimited number of cell divisions, and with each division, they produce at least one daughter cell that maintains this indefinite capacity for cell division…they can also produce progenitor cells that have finite division capacity, ultimately differentiating into the mature cell types.

The option of unlimited self-renewal of adult stem cells parallels the depicted ongoing model oscillations within the health territory. The stem cell-generated progenitor cells, which are endowed with a finite number of cell divisions, correspond to the model's path outside of the health territory to a new singularity of differentiation.

The distinction between the adult stem cell oscillations and the progenitor cell oscillations is evident in the cellular energy focus. Among the adult stem cells, the primary focus is on reproduction/cell division without much of other cellular functionality. On the other hand, progenitor cells, with their target-specific function, have only a limited potential for reproduction. Cellular energy distribution seems to be a zero-sum game.

3. Discussion

The main feature of this model is its ability to express various cycles of living entities as an interrelated and a multifunctional system. It connects concepts of systems, complexity, and chaos with features of stability and instability, linearity and nonlinearity, bifurcation, attractor, etc., each constituting an important feature of one of the main theories. This model identifies an optimal zone of function, the healthy territory, where the principles of deterministic chaos of nonlinear dynamics operate. For vigorous functioning of a system, a healthy balance between order and variability needs to exist, a result of successful resolutions of recurring transitions from linearity to positive or negative exponentiality. Outside of this health territory, there exists a significant risk to a living system.

The principles of this model may be applicable to an entire range of living entities, from stem cells to a human body. By extrapolation, similarities may also be seen in the fields of physics, business, and psychology with model polarity encompassing inflation/deflation, anxiety/depression, peace/war, etc. as expressions of exponentiality/entropy. Even the science of organizational management embraced a biologic system to formulate the latest organizational theory, called an organismic theory [14]. The primary importance of relationships vs components is emerging even in the realm of physics with a new theory, the loop quantum gravity, which stresses that it's the interaction of relationship that makes the visible world and not the accumulation of separate components [15]. It is the General System Theory that offers a theoretical path to integration of advances in various disciplines through its concept of isomorphism. It implies that some principles discovered in one discipline can be transferred to another which is still searching for a similar understanding. Bertalanffy [3] stated that “with the transfer of principles from one field to another…it will no longer be necessary to duplicate or triplicate the discovery of the same principles in different fields isolated from each other.”

One of the key characteristic of a system is the focus on the contextual importance of patterned relationships with a range of potentialities which eventually coalesce into a system's emergence. System's stability depends on the quality and the quantity of relationship interactions reflecting the degree of relativity among various components. In an open system, system's balance is not just a reflection of its internal relationships (self-organization) but also its larger external relationships (self-adaptation) to an even larger system. Redundancy is needed to maintain resiliency of a system. With diminishing redundancy, resiliency falters. In general, this is true in the early and latter phase of biologic entity's oscillation expressed in this model. Redundancy is greatest in the health territory and diminishes toward the periphery of this model. The relationship between redundancy and resiliency permeates biology. Cells have different capacity for function and repair or multiplication. A reciprocal relationship exists between functionality and repair/multiplication, because as one increases the other diminishes.

The difference between current single-target cancer therapy and system's approach to cancer control can be highlighted by Ashby's theorem of requisite variety that states that “…for effective control the variety available to the controller should be the same as the variety available to the system to be controlled” [16]. The implications of this theorem are significant due to the fact that a complex system “…to be controlled has n variables [and therefore] the controller must be able to control all n variables in order to avoid the significant risk of leaving some subset of those variables uncontrolled” [16].

The enormity of controlling all cancer variables, as looked at through Ashby's theorem, can be seen in considering the number of potential genetic and proteomic variations (30,000 genes and thousands of potential proteins from each gene). This exponential number does not even include the essential relationships among genes, proteins, and so on.

How does this model fit with other observed biologic phenomena, for example, the observed doubling of secondary cancers in patients following stem cell transplantation for leukemia or myelodysplastic syndrome [17]? This model would indicate that the introduction of stem cells, with their dual growth potential, into a larger system could, on one hand, shift the balance of system's oscillations toward the outer edge of chaos and increase the potential for cancer growth, and on the other hand, it could choose the path of stability through differentiation.

4. Implications for cancer control

Systems in chaos are amenable to stabilizing change through a process of differentiation. Similarly, systems descending into entropy, could be rescued by increasing their complexity. The described model offers potential corrective pathways out of system's undesirable states. First, there is a need, however, to recognize where a system is within the model. Is it in chaos, zone of order, or entropy? This classification leads to the selection of the most appropriate framework for looking at the observed phenomena: linear thinking is best suited for the zone of order but nonlinear thinking is most appropriate for the zone of chaos and entropy.

To stop the undifferentiated exponential growth leading to cancer and the disorderly complexity of the zone of chaos, the system has to be reset to induce differentiation and be brought back to orderly complexity. In order to restrain the limitless multiplication of cancer stem cells, which are devoting all of their energy endowment to reproduction, there needs to be a change from their singularity of oscillation to a new singularity of differentiation. This would divert the finite cellular energy from pure reproduction to a better balance between function and repair/multiplication. This could be accomplished through a process of increasing cellular function leaving only limited energy for reproduction. This concept would imply that there is a need for reorientation of treatment principles from cellular killing (cyto-toxic therapies) to cellular retraining (cyto-education). Cyto-toxic therapies, capable of eliminating 100% of cancer stem cells, have so far proven elusive. Physical activity and melatonin have been shown to facilitate the change-over process to differentiation [18-20]. Laufs et al [21] stated that “Physical activity increases the production and circulating numbers of endothelial progenitor cells…[and has] antiapoptotic effect.” Also, Takahashi et al [22] confirmed that “Exercise plays a pivotal role in myoblast differentiation.”

Additional experimental evidence also suggests that a process of changing the undifferentiated growth of cancer stem cells to differentiated normal cells, may be a valid concept. Piccirily and Vescovi [23] and Vescovi et al [24] demonstrated that bone morphogenetic proteins are capable of arresting the development of brain tumors. They showed that cancer stem cells can be redirected to develop into normal supportive cells.

To stop the link between entropy during senescence and degenerative/inflammatory diseases and/or cancer, the system has to improve its orderly complexity and self-organization. Evidence indicates that upregulating genes associated with longevity, the sirtuins, not only prolongs the life cycle but simultaneously suppresses oncogenes leading to lower cancer incidence. Experimental evidence already demonstrated that upregulation of the longevity genes does downregulate tumor genes, opening a potential avenue for modifying the historic correlation between aging and cancer incidence [9]. Other studies showed that longevity genes can be upregulated with caloric restriction, resveratrol, and physical activity [25; 26]. It has been demonstrated experimentally that aging-associated diminution of progenitor cell divisions in the brain, can be reversed by “encourage[ing] stem cells in the brain to divide…using behavioral modification techniques, such as physical exercise” [27].

If we accept that cancer is a reflection of a failing system, preventive steps should involve rebalancing the entire system through lowering of disorderly complexity, entropy, and optimizing self-organization with orderly complexity. To interrupt the strong correlation between aging and cancer, a system's view would encourage focusing on maintaining the system's rate of change through the creation of a high degree of organized complexity, and make every effort to remain as a functioning open system. A healthy life needs a great variety with a degree of unpredictability in order to keep the complex adaptive system adapting.

5. Summary

The described model confirmed the research questions that systems science, complexity, and chaos theory can be applied to biologic entities. Such theories are considered helpful in understanding of normal and abnormal cellular growth including cancer which is now seen as a system-in-failing. These theories also point to a potentially new therapeutic paradigm of cancer control: changing disorganized complexity into an organized one through increasing differentiation, decreasing entropy by increasing complexity, and strengthening self-organization and self-adaptation of biologic entities.

Conflict of interest

The authors have declared that no conflict of interest exists.

References

1. Capra F. The Web of Life. New York, USA: Anchor Books. 1996:4-138

2. Leaf C. Why we're losing the war on cancer. Fortune. 2004 :76-92

3. Bertalanffy L. General system theory. New York, USA: George Braziller. 1969:68-163

4. Waldrop M. Complexity. New York, USA: Simon & Schuster. 1992:1-145

5. Kornberg R. http://nobelprize.org/nobel_prizes/chemistry/laureates/2006/press.html

6. Fodde R. Stem Cells and Metastatic Cancer: Fatal Attraction? PLoS Med. 2006;3(12):e482

7. Laszo E. The systems view of the world. Cresskill, NJ: Hampton Press. 1996:30

8. Ashraf N, Zino S, MacIntyre A, Kingsmore D, Payne AP, George WD, Shiels PG. Altered sirtuin expression is associated with node-positive breast cancer. Br J Cancer. 2006;95:1056-1061

9. Goymer P. Ageing: Longevity mutations inhibit tumours. Nature Reviews Genetics. 2006;7:742-743

10. Kurzweil R. The singularity is near. New York, USA: Penguin Group. 2005:90-155

11. Ludwig C. Beiträge zur Kenntnis des Einflusses der Respirationsbewegungen auf den Blutlauf im Aortensystem. Arch Anat Physiol Leipzig. 1847;13:242-302

12. Goldberger AL, Rigney DR, West BJ. Chaos and Fractals in Human Physiology. Scientific American. 1990;262(2):42-9

13. Tan BT, Park CY, Ailles L, Weissman IL. The cancer stem cell hypothesis: A work in progress. Laboratory Investigation. 2006;86:1203-1207

14. Hatch M. Organization theory. New York, USA: Oxford University Press. 1997:1-376

15. Smolin L. http://www.edge.org/3rd_culture/smolin03/smolin03_index.html

16. Warfield J. Linguistic adjustments: Precursors to understanding complexity. Systems Research and Behavioral Science. 2004;21:128

17. Tanne JH. Second cancers more common in people who receive donor stem cell transplants. Br Med J. 2006;333:1140

18. Sainz R, Mayo J, Tan D, Lopez-Burillo S, Natarajan M, Reiter R J. Antioxidant activity of melatonin in Chinese hamster ovarian cells: Changes in cellular proliferation and differentiation. Biochemical and Biophysical Research Communications. 2003;302(3):625-634

19. Slattery M, Murtaugh M, Caan B, Ma K, Wolff R, Samowitz W. Associations between BMI, energy intake, energy expenditure, VDR genotype and colon and rectal cancers (United States). Cancer Causes and Control. 2004;15:863-872

20. Blask D, Dauchy R, Sauer L. Putting cancer to sleep at night: The neuroendocrine/circadian melatonin signal. Endocrine. 2005;27(2):179-188

21. Laufs U, Werner N, Link A, Endres M, Wassmann S, Jurgens K, Miche E, Bohm M, Nickening G. Physical training increase endothelial progenitor cells, inhibits neointima formation, and enhances angiogenesis. Circulation. 2004;109(2):220-6

22. Takahashi M, Kubota S. Exercise-related novel gene is involved in myoblast differentiation. Biomed Res. 2005;26(2):79-85

23. Piccirillo SGM, Vescovi A L. Bone morphogenetic proteins inhibit the tumorigenic potential of human brain tumour-initiating cells. Nature. 2006;444:761-765

24. Vescovi A L, Galli R. and Reynolds B A. Brain tumour stem cells. Nature Rev. Cancer. 2006;6:425-436

25. Ingram DK, Zhu M, Mamczarz J, Zou S, Lane MA, Roth GS, deCabo R. Calorie restriction mimetics: an emerging research field. Aging Cell. 2006;5(2):97-108

26. Keilbronn LK, de Jonge L, Frisard MI. et al. Effect of 6-month calorie restriction on biomarkers of longevity, metabolic adaptation, and oxidative stress in overweight individuals: A randomized controlled trial. JAMA. 2006;295(13):1539-48

27. Hattiangady B, Shetty A. Aging does not alter the number or phenotype of putative stem/progenitor cells in the neurogenic region of the hippocampus. Neurobiology of Aging. 2006 [Epub ahead of print]

Author contact

Correspondence to: Ivo P. Janecka, MD, MBA, PhD, 333 Westbrook Rd, St. Helena Island, SC 29920, janeckaharvard.edu. Telephone: 843-838-3602

Received 2007-3-30
Accepted 2007-5-31
Published 2007-6-5

Citation styles

©2024 Ivyspring International Publisher. Terms of use