3.2
Impact Factor
ISSN: 1449-1907
Int J Med Sci 2004; 1(1):11-20. doi:10.7150/ijms.1.11 This issue Cite
Research paper
Discriminating between elderly and young using a fractal dimension analysis of centre of pressure
1School of Biomedical and Sports Science, Edith Cowan University, Perth, WA 6027, Australia
2Biomechanics Laboratory, Ball State University, Muncie, IN 47306, USA
3Faculty of Education, Health, and Science, Charles Darwin University, Darwin, NT 0815, Australia
Received 2004-1-21; Accepted 2004-2-5; Published 2004-3-10
Abstract
The aim of this project was to evaluate the use of a new analysis technique, fractal dimension analysis, for quantification of quiet stance centre of pressure (COP). By using a fractal dimension analysis of COP, it might be possible to gain more information about control during quiet stance than traditional analyses have previously allowed. The current project considered a group of young healthy participants and a group of elderly healthy participants to compare traditional measures of COP against a fractal dimension analysis of COP. Results indicated that both types of analyses are able to distinguish between eyes open and eyes closed in the elderly group. However, the fractal dimension analysis more accurately detected differences between the participant groups when standing with their eyes closed. Based on these results it is suggested that fractal dimension analysis is more informative about posture control than traditional measures. It is suggested that a fractal dimension type of analysis can be incorporated into clinical testing to identify patients with pathologies.
Keywords: dynamical systems, quiet stance, non-linear, control, balance
1. Introduction
Centre of pressure (COP) traces derived from force readings have the potential to inform us about the control strategies used for postural stability; they are easily garnered, non-invasive, and immediate. COP traces represent the movement of a person about a stable position in both the sagittal and frontal planes. Provided that a person's COP remains within allowable limits, the person will remain standing upright. Difficulty lies in deciphering the information contained within these traces and distinguishing one from the other. However, with recent advances in the area of chaos and mathematics, in particular non-linear techniques for analysis, fractal patterns of natural phenomena are being revealed. A fractal pattern gives description to irregular shapes such as COP traces, and provides us with a means to describe them in opposition to the traditional thinking that these patterns are derived from some random mechanism. Currently there is a paradigm shift towards recognising the chaotic properties of natural phenomena and the use of appropriate non-linear analysis, such as fractal analysis, in place of traditional analyses [1] .
A strong reason behind this paradigm shift is the acknowledgment of variability in natural systems to be healthy and, in fact, desirable. In other natural systems such as control of heart rate, heartbeats do not occur at regular intervals but at seemingly random intervals. Similarly, when asked to walk on a treadmill, stride lengths and frequencies are just slightly unevenly spaced. Such variability in these systems allows for accommodations to external perturbations, for more regular systems even the slightest perturbation can lead to a complete breakdown of the system e.g., a fall following a trip during gait versus a stumble to recover. Many researchers assume this variability to be a super-imposed noise on an otherwise regular signal [2, 3] . However, this view is being opposed in the literature and rather a variable signal is now viewed as natural [4, 5, 6] .
New methods for quantifying signal variability are needed in order to determine the affects of such variability. Higuchi [7] has provided a relatively straight-forward technique that can be applied to time-series data to extract the fractal dimension. When applied to data such as COP displacement, a fractal dimension will be reported that lies between 1 and 2. Data with no variability, for example the unlikely situation where a person is standing completely stationary with no postural sway, will have a fractal dimension of 1. Typical COP data that has been filtered using standard methods e.g., Butterworth low pass filters, will also have a fractal dimension tending towards 1. In this case, the natural variability of a signal has been removed and as a result the complexity of the signal has been lost due to inappropriate treatment of the data. What remains are the gross movements associated with quiet stance COP, but the subtleties have been lost. For data that has been randomly generated or data with too high a noise component the fractal dimension will tend towards 2, indicating that the signal is indiscriminately wavering about its underlying signal.
Peng, Hausdorff, and Goldberger [8] have demonstrated that normal human gait has a robust fractal pattern. This fractal pattern is disturbed when one is asked to walk in time to an outside timing mechanism instead of one's own 'internal clock'. Yamada [4] used a type of non-linear analysis that is analogous to the fractal dimension, the Lyapunov exponent, and determined COP data to be chaotic while five participants both a) stood still, and b) swung their arms while standing still. Earlier, Collins and De Luca [9] had determined COP trajectories to be stochastic, modelling these trajectories as random (non-deterministic) motion. The research of Yamada [4] opposed this view and successfully demonstrated that COP trajectories are in fact chaotic (deterministic). Blaszczyk and Klonowski [10] performed a non-linear analysis of 12 healthy elderly participants' COP data and found that a fractal dimension analysis, using Higuchi's algorithm revealed a difference between participants when they stood a) with their eyes open, and b) with their eyes closed. COP patterns were determined to have a higher fractal dimension when eyes were closed compared to standing with eyes open. It is important to note, that in this study, a loss of visual information while standing is accompanied by a significant increase in the fractal dimension of the COP. This implies that an increase in the fractal dimension of the COP during quiet stance may be an indicator of postural instability or the use of less stable control strategies. Most recently, Harbourne and Stergiou [11] investigated COP of infants in three different stages of sitting postural development. Using non-linear analysis techniques including: the Lyapunov exponent, correlation dimension, and approximate entropy, these researchers showed that the development of an infant's sitting postural control is not only a dynamic process but one that agrees with Bernstein's [12] proposition that the development of natural systems involves controlling the degrees of freedom inherent in the system. In the case of infants developing their control of sitting posture, the first stage of development was characterised by constraining the degrees of freedom to control the system, and subsequent releasing of these degrees of freedom allowing for greater adaptability to their environment. These findings from Harbourne and Stergiou [11] provide further evidence opposing Collins and DeLuca's [9] suggestion that natural systems, such as those responsible for postural control are the consequence of stochastic processes. If we accept that variability in natural systems, such as COP control, is normal then a deviation away from a fractal pattern may be indicative of a shift towards an unhealthy or less desirable control strategy. The analysis of fractal patterns in gait and posture data may serve as an indicator of pathology or impairment. Surrogate data analysis is used to test for a system's non-linearity. This check for non-linearity via the use of surrogate data analysis has been used widely in the past and most recently to assess the variability of gait data in the elderly [6] . Together with the above research that has identified non-linearity in natural systems, surrogate data analysis provides a means by which to determine if non-linear analysis techniques are warranted, if not necessary. This surrogation process involves reconstructing new data sets from these original data; results from both data sets are compared to each other. If the results are significantly different from each other, then non-linear analysis of the original data can be considered appropriate.
Recently Parkinsonian patients (PP), spinocerebellar ataxia (SCA) patients, and healthy participants' COP were analysed using a more traditional fractal dimension analysis [13] . This method recorded COP data and analysed COP traces using an image analyser to calculate the fractal dimension directly from the image, as opposed to a time series data analysis such as in Higuchi's method. Their findings demonstrated that a higher fractal dimension was calculated from the COP data for the PP and SCA groups compared to the normal population. Further, with a more severe clinical stage of disease the fractal dimension also increased while the more traditional measures showed no change. Their conclusion from these findings were that a fractal dimension analysis of COP data is more sensitive than traditional measures and that it may provide a good screening tool or measure of disease progression. The disadvantage of this type of fractal analysis is that it uses the images of the COP that are then digitised and analysed using a commercial image analyser. Compared to Higuchi's algorithm this technique is far more involved and time consuming.
With advances being made in the theoretical understanding and practical application of non-linear analysis techniques, it is important that researchers begin to examine appropriate data using such techniques. In particular, a non-linear approach to the analysis of COP data may be appropriate and may reveal information regarding a person's control of their upright posture that has not previously been discovered. It is well accepted that with age our mechanisms for controlling upright posture deteriorate and that often, in the absence of visual information, at least in the elderly, similar detriments to upright posture are observed [14, 15] . The aim of this study was to examine both the effects of age and loss of visual information on control of COP during quiet stance and to evaluate the use of Higuchi's algorithm for this purpose. Specifically, fractal dimension results were compared to traditional measures of COP to determine the efficacy of using Higuchi's algorithm for quiet stance COP analysis.
2. Method
Participants
Ninety-one participants from the surrounding community volunteered to participate in this study. They were grouped according to age with seventy-four young; 21.5(2.8) years, 1.72(0.1) m, and 73.8(17.1) kg, and seventeen elderly; 69.5(6.2) years, 1.72(0.1) m, and 82.0(17.9) kg, healthy adults. Participants reported having no existing lower limb injuries or pathologies, or balance disorders, and had not undergone any major lower limb surgery. The research protocol was reviewed by and received ethical clearance from the university Institutional Review Board committee. All participants signed an informed consent document.
Procedure
Participants were tested in one session and stood quietly for two minutes with their eyes closed (EC) and two minutes with their eyes open (EO). The sequence of presentation was randomised to eliminate order effects. Force data, collected at 20 Hz, were measured using a Kistler force plate (type 9281B, Kistler Instrumente AG, Winterthur, Switzerland) to provide anterior/posterior (A/P) and medial/lateral (M/L) COP data. Participants were not instructed as to where or how to place their feet on the force plate. Because the aim of the study was to assess normal quiet stance, self-selected foot placement was considered to be most appropriate.
Analysis
Surrogate data
[16] Surrogate data analysis provides a test for non-linearity of data to determine if non-linear techniques may be appropriately applied. This process uses the original time series and, in the present case, employed a technique known as the amplitude adjusted Fourier transform (AAFT) algorithm. The surrogate data created by the AAFT algorithm had the same amplitude distribution as the original time series but had been appropriately re-ordered to represent a signal created by a linear Gaussian process. Results from the original data were compared to results from these surrogate data using paired t-tests to assess the appropriateness of applying non-linear techniques to the data.
Fractal dimension
Using Higuchi's algorithm [7] the fractal dimension was calculated using custom written software in Matlab (The Mathworks Inc., Natick, MA, USA). This method for calculating the fractal dimension is designed specifically for use with time series data such as COP data. From the original data a number of new data sets were reconstructed according to Higuchi's algorithm. The number of data sets reconstructed (k-max) was determined by the researcher. For each reconstructed data set the curve length was calculated and plotted against its corresponding k value on a log-log scale. The resulting slope, fitted by a least-squares method, represents the fractal dimension of the original data. Determining k-max was by a process of examining the data and plotting the fractal dimension over a range of k-max; the point at which the fractal dimension plateaus was considered a saturation point beyond which no benefit could be gained from further calculations. Best results for the current data were obtained using a k-max value of 60 for A/P analysis and 30 for M/L analysis (cf. [17] ). The fractal dimension was calculated over the entire two minute epoch using all data points.
Traditional measures
Range of sway in A/P and M/L directions was calculated as the difference between the maximum and minimum excursions. The maximum first time derivative of the displacement in each direction provided peak sway velocities. Finally, a temporal summing of the product of movement in each direction provided the total excursion area.
Statistics
Paired-samples t-tests were used to determine significance of within group differences between conditions. Independent-samples t-tests determined significance of between group differences for the same condition. An alpha level of 0.05 was used as the criterion for significance of effect. Levene's test for homogeneity was performed on all data sets.
3. Results
Surrogate analysis
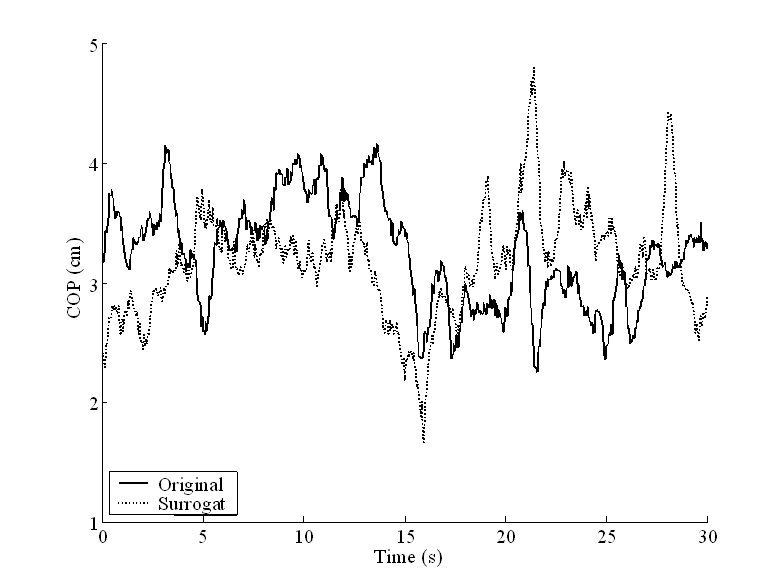
Across both groups and conditions the surrogate analysis produced significantly higher fractal dimensions (p < 0.05). The calculated surrogate fractal dimensions for the young and elderly were [mean(SD)] EO = 1.53(0.08) and 1.54(0.06), and EC = 1.52(0.07) and 1.60(0.08), respectively. Since the main findings were in the A/P direction, surrogate data sets were only calculated for this direction. For illustrative purposes original data and its associated surrogate data is displayed in Figure 1 . These findings confirm the appropriateness of a non-linear analysis of these data.
Representative data for illustrative purposes. Elderly participant data during eyes open condition. Original data in solid line, surrogate data represented by dashed line. For clarity only 30 seconds of the 2 minute data collection are presented.
Fractal dimension
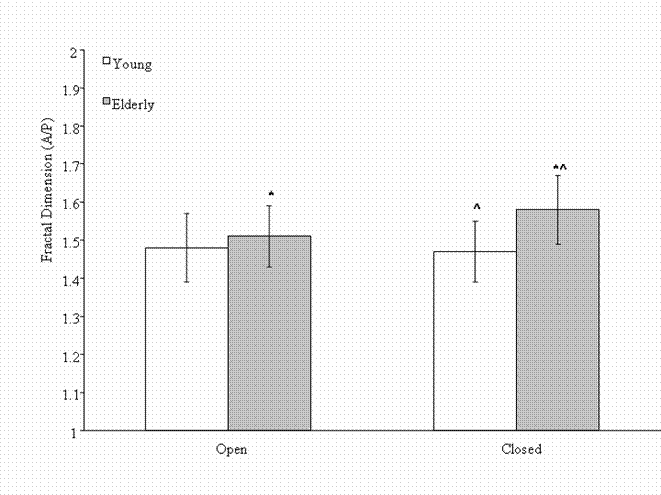
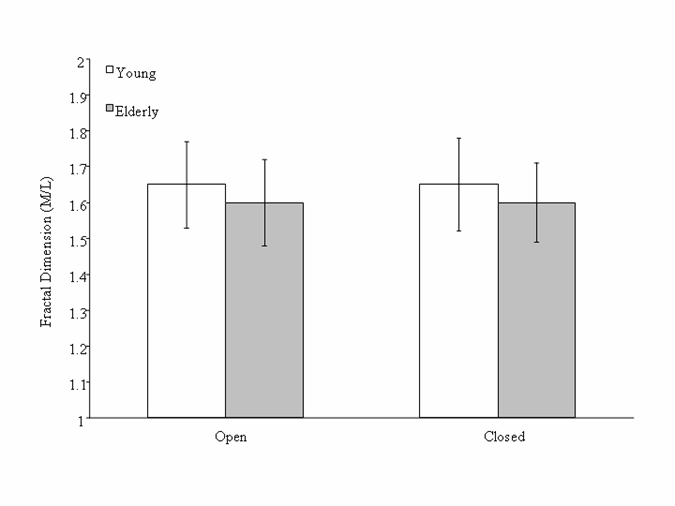
No fractal dimension differences were detected within the young group for either the A/P (EO = 1.48(0.09), EC = 1.47(0.08)) or M/L (EO = 1.65(0.12), EC = 1.64(0.13)) direction of COP (p > 0.05). The elderly group exhibited a significant increase in the fractal dimension, in the A/P direction only (EO = 1.51(0.08), EC = 1.58(0.09)), when asked to stand with their eyes closed compared to standing with their eyes open (p < 0.05). There was no significant difference in the fractal dimension of the M/L COP in the elderly group (EO = 1.60(0.12), EC = 1.60(0.11)). A between group difference existed such that the elderly group had a higher fractal dimension, in the A/P direction, than the young group when standing with eyes closed (p < 0.05). All data satisfied Levene's test for homogeneity. Results are displayed in Figures 2 and 3 .
Mean(SD) results of fractal dimension analysis of COP in A/P direction. ^ indicate a significant difference between young and elderly in the eyes closed condition; * indicate a significant difference between eyes open and eyes closed in the elderly only.
Mean(SD) results of fractal dimension analysis of COP in M/L direction. No significant differences were present.
Traditional measures
Only total excursion area exhibited significant differences between the EO (10.19(3.39) cm2) and EC (11.89(5.90) cm2) conditions (p < 0.05) for the young group. Results are given in Table I . The elderly group demonstrated similar significant differences to those shown in the fractal dimension analysis. Range and peak sway velocity in the A/P direction were significantly different between conditions (p < 0.05). These same measures in the M/L direction were not significantly different. Table II provides detailed results.
Results for traditional measures of quiet stance in the young participant group as indicated by mean(SD) . Significance denoted by *.
| Open | Closed | |
| A/P Range (cm) | 3.31(1.31) | 3.60(1.52) |
| M/L Range (cm) | 2.63(1.95) | 2.41(1.64) |
| A/P Peak Sway Vel. (cm.s-1) | 5.12(3.41) | 6.90(7.97) |
| M/L Peak Sway Vel. (cm.s-1) | 5.57(4.88) | 6.17(8.76) |
| Excursion Area (cm2) | 10.19(3.39)* | 11.89(5.90)* |
Results for traditional measures of quiet stance in the elderly participant group as indicated by mean(SD). Significance denoted by *.
| Open | Closed | |
| A/P Range (cm) | 3.27(0.76)* | 3.90(0.93)* |
| M/L Range (cm) | 2.35(0.93) | 2.15(0.81) |
| A/P Peak Sway Vel. (cm.s-1) | 5.74(1.88)* | 9.38(4.19)* |
| M/L Peak Sway Vel. (cm.s-1) | 4.33(1.07) | 4.75(1.12) |
| Excursion Area (cm2) | 9.87(2.46) | 17.53(8.33) |
Total excursion area was significantly different between the two groups when standing with their eyes closed (p < 0.05). However, Levene's test for homogeneity suggests that significant findings for this variable may be questionable (F = 5.850, p < 0.05).
4. Discussion
Young and elderly healthy adults stood with their eyes open and their eyes closed to address the issue of whether or not a fractal dimension analysis of COP data could provide information regarding quiet stance posture. Results from this research indicate that the application of Higuchi's method for fractal dimension analysis can be used to discriminate between different conditions of quiet standing and young versus old subjects. It is further suggested that a fractal dimension analysis of COP may be more informative than traditional measures used to describe COP traces.
Surrogate Analysis
The use of surrogate data analysis is common place to test for the appropriateness of applying non-linear techniques to data. Of significant interest to this investigation was the use of a non-linear analysis technique applied to quiet stance COP data. Results from the surrogate data analysis indicated that variation inherent in the COP data was not due to random fluctuations but rather, it is more likely they are the consequence of some deterministic process of control. These findings concur with a number of other researchers who have previously found deterministic structure present in COP data [5, 11] .
Fractal dimension
This research investigated the use of a fractal dimension analysis for investigating the effect of age and a loss of visual information on quiet stance COP. Blaszczyk and Klonowski [10] have previously investigated the loss of visual information in elderly participants and found the fractal dimension to significantly increase when their participants were asked to stand without visual information. These findings are supported by results from the current project. A further finding of the current project was that Higuchi's algorithm can also discriminate between the young and elderly during the no-vision condition.
During normal quiet standing with eyes open, the visual system has been demonstrated to be largely responsible for the control of upright posture in young children, but in older children and adults the reliance on visual information diminishes. This was first addressed in Lee and Aronson's [18] swinging room paradigm. Recently, Wann, Mon-Williams, and Rushton [19] further explored this idea; their results also indicated this trend for a reliance on visual information for control of posture in younger children and children with diagnosed co-ordination difficulties. It is not surprising then that results from the present study did not show significant differences when the young adult group stood with their eyes closed, compared to when they stood with their eyes open. Participants in this group may use information from their visual system to help with the control of an upright posture, but do not rely heavily on it. Instead their information for control is most likely derived from their proprioceptive and vestibular systems which they are able to reliably use in the absence of visual information. The elderly group however, did show a significant change in their fractal dimension when they closed their eyes demonstrating a larger reliance on visual information than their younger counterparts during this condition. That a difference was found between the two groups during the eyes closed condition indicates that different strategies are used by each group to control their posture when standing with their eyes closed. It is beyond the scope of this paper to hypothesise which control mechanisms are used by this group during periods without vision, although one certainty is evident from these results; there is an age-related decline in effectiveness of control mechanisms for quiet stance.
Expanding on the results of Blaszczyk and Klonowski [10] this research revealed that fractal analysis of COP data is sensitive enough to discriminate between different age-groups of participants when standing quietly with their eyes closed. It also supported their findings that an elderly population sample exhibits different non-linear properties of A/P COP across the two test conditions. It is suggested that a fractal dimension analysis may be useful for identifying unhealthy or unstable quiet stance posture.
Traditional measures
Statistical results of traditional measures of quiet stance closely matched the fractal dimension results. Measures relating to the A/P direction demonstrated significant differences in the elderly group with no differences existing in the young group. Between groups only the two-dimensional variable, total excursion area, was significantly different. However, previous research suggests that comparisons should not be made between A/P and M/L COP data as these variables act independently of each other [20, 21] . Total excursion area is a cumulative sum of the product of the distance travelled in each of the A/P and M/L directions. Therefore, although significant differences in the excursion areas between participant groups under the eyes closed condition existed, this measure may not be appropriate to describe COP. Winter et al. [20] further suggest that depending on the type of stance being investigated control of upright posture in the A/P or M/L direction changes accordingly. For example, the A/P direction may be controlled by plantar/dorsiflexion of the ankle during side-by-side stance, but be controlled by hip loading/unloading during tandem stance. Consequently, Winter et al. [20] concluded that a typical 'spaghetti' plot is neither representative nor informative about COP control. Likewise, a measure of total excursion area, it is suggested here, is also not an appropriate variable that is informative about COP control.
This research demonstrates that a fractal dimension analysis can inform about COP data equally as well as a traditional analysis of quiet stance. The current results also support the notion that the traditional total excursion area variable used for description of COP may not be a meaningful measure [20, 21] . As such, even though findings from the current experiment suggest a significant difference in the total excursion area between participant groups in the eyes closed condition, this may not be truly indicative of a between group difference. Further this statistical finding must be viewed speciously given that the data was non-homogenous. The fact that the fractal dimension and total excursion area findings match each other may only be a coincidence.
The current experimental findings support the idea that a non-linear analysis of COP is appropriate. These findings also support the suggestion of Blaszczyk and Klonowski [10] that the use of a fractal dimension analysis of COP, particularly in the A/P direction, may help to identify subtle changes associated with aging or pathologies.
General Discussion
A cursory glance of the results presented above might lead one to believe that the fractal dimension analysis, since it revealed similar results to the traditional analysis, is no better than already established methods. The reader must recall a number of points made above: recent research by Winter et al. [20, 21] suggest that the total excursion area may not be an appropriate measure of posture control and results from the total excursion did not strictly fit to standard statistical rules i.e., they were non-homogenous. Harbourne and Stergiou [11] note, in their discussion of Correlation Dimension results of sitting posture COP, that a change in this dimension suggests a freezing or releasing of the degrees of freedom in the system under investigation depending on how this measure changes. For the current non-linear measure, Higuchi's fractal dimension, where this dimension approaches 1, this is indicative of a system whose degrees of freedom have been frozen in an attempt to control itself. This is potentially a hazardous control strategy as it affords little adaptability to a changing environment. In the case of the elderly participants in the current cohort, the fractal dimension approaches 2; this can be considered to be indicative of a system whose degrees of freedom have been increased to a point where the system is dynamic but under little control, in the case of postural sway the system is swaying equally on either side of the stable position. The researchers consider an indicator of a healthy postural control strategy to be one described by a fractal dimension that lies between 1 and 2. When this is so, the participant is swaying about the stable point in a complex and dynamic manner with a high level of control of the degrees of freedom, and as such able to adapt easily and quickly to changing conditions.
5. Summary
As the notion that control systems are not governed by regular processes is realised, tools that provide insight to these processes are needed if we are to advance our understanding of movement control. A wide range of techniques are available that allow for the analysis of movement from a non-linear perspective, however many of these are complicated and may not be easily understood by those without a solid background in the associated theories. Higuchi's algorithm, presented here, is more easily presented and provides a simpler means by which to quantify a non-linear system and as such may be more readily accepted by clinicians. The potential of the fractal dimension analysis is yet to be realized and is the subject of current research by the investigators.
Conflict of interest
The authors have declared that no conflict of interest exists.
References
1. Capra F. The Web of Life: A new scientific understanding of living systems. New York: Anchor Books. 1996
2. Kay BA. The dimensionality of movement trajectories and the degrees of freedom problem: A tutorial. Hum Mov Sci. 1988 ;7 :343 -364
3. Kelso JAS, Schoner JP, Haken H. Phase-locked modes, phase transitions, and component oscillators in biological motion. Phys Script. 1987 ;35 :79 -87
4. Yamada N. Chaotic swaying of the upright posture. Hum Mov Sci. 1995 ;14 :711 -726
5. Yamada N. Nature of variability in rhythmical movement. Hum Mov Sci. 1995 ;14 :371 -384
6. Buzzi UH. et al. Nonlinear dynamics indicates aging affects variability during gait. Clin Biom. 2003 ;18 :435 -443
7. Higuchi T. Approach to an irregular time series on the basis of the fractal theory. Phys D. 1988 ;31 :277 -283
8. Peng CK, Hausdorff JM, Goldberger AL. Fractal mechanisms in neural control: Human heartbeat and gait dynamics in health and disease. In: (ed.) Walleczek J. Nonlinear Dynamics, Self-Organization, and Biomedicine. Cambridge: Cambridge University Press. 1999 :-
9. Collins JJ, De Luca CJ. The effects of visual input on open-loop and closed-loop postural control mechanisms. Exp Brain Res. 1995 ;103 (1) :151 -63
10. Blaszczyk JW, Klonowski W. Postural stability and fractal dynamics. Acta Neuro Exp. 2001 ;61 :105 -112
11. Harbourne RT, Stergiou N. Nonlinear analysis of the development of sitting postural control. Dev Psychobiol. 2003 ;42 (4) :368 -377
12. Bernstein N. The co-ordination and regulation of movements. London: Pergamon Press. 1967
13. Manabe Y. et al. Fractal dimension analysis of static stabilometry in Parkinson's disease and spinocerebellar ataxia. Neurol Res. 2001 ;23 :397 -404
14. Hughes MA. et al. The relationship of postural sway to sensorimotor function, functional performance, and disability in the elderly. Arch Phys Med Rehabil. 1996 ;77 (6) :567 -72
15. Teasdale N, Simoneau M. Attentional demands for postural control: the effects of aging and sensory reintegration. Gait Posture. 2001 ;14 (3) :203 -10
16. Theiler J. et al. Testing for nonlinearity in time series: the method of surrogate data. Phys D. 1992 ;58 :77 -94
17. Accardo A. et al. Use of the fractal dimension for the analysis of electroencephalographic time series. Biol Cybern. 1997 ;77 :339 -350
18. Lee DN, Aronson E. Visual proprioceptive control of standing in human infants. Percept Psychophys. 1974 ;15 :529 -532
19. Wann JP, Mon-Williams M, Rushton K. Postural control and co-ordination disorders: The swinging room revisited. Hum Mov Sci. 1998 ;17 :491 -513
20. Winter DA. et al. Unified theory regarding A/P and M/L balance in quiet stance. J Neurophysiol. 1996 ;75 (6) :2334 -43
21. Winter DA. et al. Motor mechanisms of balance during quiet standing. J Electromyogr Kinesiol. 2003 ;13 (1) :49 -56
Author biography
Tim Doyle is a Doctoral student at Edith Cowan University in Perth, Australia. His current research interests include risk assessment of falls in the elderly.
Eric Dugan is currently Director of the Biomechanics Lab at Ball State University, Muncie, Indiana. His current research investigates musculo-tendinous stiffness and its affects on injury risk, performance, and neuromuscular control.
Brendan Humphries lectures in Biomechanics at Charles Darwin University in Darwin, Australia. His particular line of research is aimed at understanding the effects that aging has on bone, and the potential benefits of vibration on enhancing bone in this group.
Robert Newton is Foundation Professor at Edith Cowan University in Perth, Australia. His research incorporates investigations into the benefits of exercise, particularly resistance training, on the elderly population.
![]() Corresponding address:
Corresponding address:
Mr. Tim Doyle, School of Biomedical and Sports Science, Edith Cowan University, 100 Joondalup Drive, Joondalup, Perth, WA, 6027. Phone: (Int+61)(8) 9400-5097. Email: t.doyleedu.au

 Global reach, higher impact
Global reach, higher impact