3.2
Impact Factor
ISSN: 1449-1907
Int J Med Sci 2014; 11(5):508-514. doi:10.7150/ijms.8249 This issue Cite
Research Paper
Tuberculosis Disease Diagnosis Using Artificial Immune Recognition System
1. Department of Computer Science, Chalous Branch, Islamic Azad University (IAU), 46615-397 Chalous, Mazandaran, Iran;
2. Department of Health Services Administration, Science and Research Branch, Islamic Azad University, Shiraz Fars, Iran;
3. Department of Computer Engineering, University of Guilan, Iran.
4. Faculty of Science and Technology, Bournemouth University, UK.
5. University of Niš, Faculty of Mechanical Engineering, Department for Mechatronics and Control, Aleksandra Medvedeva 14, 18000 Niš, Serbia.
6. Department of Computer System and Technology, Faculty of Computer Science and Information Technology, University of Malaya, 50603 Kuala Lumpur, Malaysia.
Received 2013-11-30; Accepted 2014-3-5; Published 2014-3-29
Abstract
Background: There is a high risk of tuberculosis (TB) disease diagnosis among conventional methods.
Objectives: This study is aimed at diagnosing TB using hybrid machine learning approaches.
Materials and Methods: Patient epicrisis reports obtained from the Pasteur Laboratory in the north of Iran were used. All 175 samples have twenty features. The features are classified based on incorporating a fuzzy logic controller and artificial immune recognition system. The features are normalized through a fuzzy rule based on a labeling system. The labeled features are categorized into normal and tuberculosis classes using the Artificial Immune Recognition Algorithm.
Results: Overall, the highest classification accuracy reached was for the 0.8 learning rate (α) values. The artificial immune recognition system (AIRS) classification approaches using fuzzy logic also yielded better diagnosis results in terms of detection accuracy compared to other empirical methods. Classification accuracy was 99.14%, sensitivity 87.00%, and specificity 86.12%.
Keywords: Artificial Immune Recognition System, Fuzzy system, Tuberculosis, Safety.
1. Introduction
The main microorganism in tuberculosis is Mycobacterium tuberculosis [1]. In this infectious disease, the microorganisms frequently penetrate into the lungs (through breathing) and are spread to the whole body through the blood circulatory system, lymphatic system or direct extension to other organs. Tuberculosis bacteria are spread into the air when contaminated person spit, talk, sneeze or cough. A person needs only to inhale a small number of these bacteria to become infected. There may be high risk of becoming infected if the intensity of exposure to the bacteria is high and for a long time [2, 3].
Typical outward indications of pulmonary tuberculosis include persistent cough, weight reduction, occasional fever, coughing blood and night sweats [4]. Tuberculosis evolves in the human body in two phases. The first phase occurs when someone who is subjected to micro-organisms from a contagious case of tuberculosis becomes infected (tuberculosis infection), and the second is when the infected person grows the illness (tuberculosis). TB is a significant cause for illness and death worldwide, especially in Asia and Africa. It is an immense problem in most low income countries, and it is the single most frequent cause of death in children in particular [5]. Based on a government health ministry statistics report in 2006, an estimated 23.875 patients have tuberculosis each year, of which 3.448 die in the world [6].
Varieties of machine learning based models have been proposed for performing clinical diagnostics. For instance, a standard instrumentation for building multivariate diagnosis models is discrimination analysis, specifically for operating on linear systems [7, 8]. According to the literature, Multilayer forward neural networks in addition to back-propagation neural networks are a decent, effective analysis tool for complex nonlinear systems [9, 10]. Despite the fact that the precipitous descent method is implemented to amend the weights, it underperforms because of its slow convergence rate and suboptimal solutions [11, 12]. Volatile organic compounds (VOCs) in the breath may change using the Fuzzy logic-based pulmonary tuberculosis diagnosis because Mycobacteria and oxidative stress are the outcome of Mycobacterial infection, both of which develop distinctive VOCs [13]. Pulmonary tuberculosis and its important characteristics assist with the constitution of a classification model for TB diagnosis. On the other hand, the detection outcome of such model is not accurate.
To mitigate the tuberculosis diagnosis problem, different classification systems have been used. For example, Philips et al. [13] reached 82.6% classification accuracy with fuzzy classification methods. Porcel et al. [14] obtained 97.45% accuracy using 10-fold cross validation with a C4.5 decision tree procedure. The accuracy obtained by Er et al. [9], who used neural networks, was 95.08%, while Ansari et al. obtained 96% accuracy with Neuro-fuzzy for tuberculosis diagnosis [15]. Chang et al. [16] utilized support vector machines with high accuracy, with average precision of 89.2%. A variety of related algorithms have been introduced to address this problem, such as fuzzy classifiers [17] and support vector machines [18]. A number of researchers have carried out comparative studies on reinforcement learning algorithms.
Lately, an innovative intelligent method called Artificial Immune Systems (AISs) has been implemented on different platforms and applications specifically in the field of pattern recognition [19], [20], [21], and [22]. The model in [23, 24] simulated the competition between the immune system and the mammary carcinoma under the action of an external force field (the vaccine). The mathematical model proposed in this paper was based on nonlinear ordinary differential equations. Cells in the immune system are able to accomplish very complicated tasks include learning, ability to categorically separate other host's entities (self) and foreign or infected selves (non-self), advancing in time to function better and achieve better results, in addition to those they can retain memories of previous encounters for faster response in the case of repeating infections this acquiring capacity persistently improve their reactive potential. Illustrated model in [25] explains the mutated cells and their improvement toward more sophisticated levels of mutation, and compared them with immune system cells, when they are able to detect mutated cells and kill them. The essential concept behind AIS is the implementation of a proctor learning procedure to generate a core data point to embody the repartition space for each distinct class. Subsequently, these represented points of data would be implemented to make a template of breeding future. Nonetheless, the success of this method rests on the core data points carefully chosen by the AIS system. At the moment the AIS makes memory cells, the k-NN models only use these points for specimen predictions. Exclusive of additionally considering any other possibly useful information from the entire existing data, this phenomenon may cause unreliable prediction results.
In this paper, the artificial immune recognition system (AIRS) process with fuzzy labeling is used to form an unsupervised learning AIRS approach and to substantiate tuberculosis diagnosis identification. By using the independent clinical tuberculosis diagnostic data sets from the Pasteur Lab in North Iran and patient epicrisis studies, the aim is to show the benefits of the proposed AIRS and fuzzy method around the standard bio-inspired method to provide a machine learning decision support system to assist health practitioners with their diagnosis conclusions. The results are compared against previous studies reported that focused on tuberculosis diagnosis with two commonly used neural network models, and suggestions are made for future applications of this new method.
The rest of the paper is structured as follows. Section 2 provides the materials description, including the tuberculosis disease dataset. Previous research works in related areas and a brief outline of artificial immune recognition systems are discussed in Section 3. Section 4 addresses the proposed Fuzzy method for feature labeling. The measures for performance evaluation are explained in Section 5 with classification accuracy, specificity, sensitivity, and cross validation. The experimental results achieved in TB detection are given in Section 6. Finally, Segment 7 concludes the paper with a summary of outcomes, highlights on the significance of this study as well as indications for future work.
2. Material description
For this study, patient epicrisis reports from the Pasteur Laboratory located in North Iran were employed. A dataset was prepared using these epicrisis reports, which consists of tuberculosis disease measurements containing two classes and 175 samples. For the experiments, 70% of the data was used to train samples and the subsequent 30% to test samples. The class distribution is as follows: Class 1: Tuberculosis (114); Class 2: Normal (60). All samples have twenty features which collect from laboratory: Complaints of cough, Chest pain, Leukocyte count (WBC), Weight loss, Night sweats, Fever, Shortness of breath, HIV, PPD, CD4, Hemoglobin concentration (HBC), Platelet count, Neutrophil count (NC), Lymphocyte count, Erythrocyte sedimentation rate (ESR), Alanine aminotransferase (ALT) level, Alkaline phosphatase (ALP) level, Lactate dehydrogenase (LDH) concentration, and Albumin [7] concentration. A summary of the statistical properties in the tuberculosis database is provided in Table 1.
Statistical properties of tuberculosis database
| Input parameters | Average value | Standard derivation | Maximum value | Minimum value |
|---|---|---|---|---|
| Ā | (σ) | (xmax) | (xmin) | |
| Hemoglobin | 11.33 | 2.82 | 16.80 | 6.16 |
| Platelet | 394.57 | 201.84 | 818.00 | 49.00 |
| WBC | 9.84 | 5.49 | 22.70 | 1.33 |
| Neutrophil | 8.62 | 6.08 | 21.98 | 1.00 |
| Lymphocyte | 1.66 | 1.25 | 5.00 | 0.02 |
| Erythrocyte sedimentation | 50.36 | 40.36 | 125.00 | 1.00 |
| Alanine aminotransferase | 140.04 | 117.62 | 377.00 | 8.00 |
| Alkaline phosphatase | 493.44 | 495.33 | 1629.00 | 31.00 |
| Lactate dehydrogenase | 1091.17 | 780.15 | 2616.00 | 210.00 |
| Albumin concentration | 3.17 | 1.25 | 5.00 | 1.02 |
3. Description of the Method
3.1. The Artificial Immune System (AIS)
Artificial Immune Systems (AISs) have been described as a new part of computational sciences that emerged in the 1990s. It attempts to simulate biological behaviours by using genetic algorithms based artificial neural networks. The inspirations behind AIS systems are theoretical immunology, immune system's functions and models, AIS systems apply these concepts to complicated problems [26]. Numerous information-processing applications are benefiting from AISs' concepts (e.g. feature extraction, pattern recognition, machine learning and data mining [27, 28]). Fuzzy models serve as a representation method of immune system cells and are applied in several AISs [29]. Furthermore, artificial immune system (AIS) is used for medical diagnosis [22, 27, 30]. The following is a demonstration of an effective AIS algorithm.
3.11. Initialization
In this research, major Artificial Immune Systems (AIS) terms are defined using common terms from the biologic immune system. AIS originates by the antigens, the representative data points are memory cells and artificial recognition balls [16] are defined as a set of nominated memorial cells.
Step (0) entails the preprocessing and initializing phase for the proposed algorithm. Sample data vectors are regularized in this stage, such that the distance between two data vectors for both cases of antigen and ARB members will be in a close range of (0,1). In this research, a base memory cell and ARB population are set for each training sample (antigen).
3.12. ARB Generation
Step (1) is a process of detecting memory cells (mc) originating in a similar category as the antigen (ag) and imitated by antigen. The basic definition of stimulation is “1- Dist (ag, mc)” where “Dist” is a mathematical Euclidean distance among the two selected vectors. The shorter the distance is, the more stimulation effects there are. The identified memory cell is represented as mc_mtach.
In Step (2) the memory cell is cloned at a predefined clone rate of (μ). In the meantime, as memory cells have similar data construction and a similar number of dimension numbers as the training data, every individual feature of the clones can mutate with a definable mutation rate of (ζ) to protect the variety of memory cell candidate applicants. In the last part of this stage, the algorithm adds these new clones to the existing ARB population.
3.13. The Process of Nomination of New Memory Cells
The main challenge is that all ARB members create new memory in rival mode. Step (3) is the resource allocation process where (ψ) will be practically applied to the ARB population, which relates to the stimulus level of each individual ARB member of the current antigen.
The ARBs with greater motivation will be provided with more of the limited resource. This procedure will cause the death and demise of some ARB members who show lower stimulation responses. This part of the process will in turn control the ARB population.
In Step (4) the average stimulation of the ARB population of each class is computed, and if it is greater in comparison to a user-defined threshold value of (δ) the learning process of this antigen system will stop. Step (5) signifies the start of randomizing the mutation and cloning the surviving ARB members with a statistical probability in a way that is proportional to their simulation level, after which a return to step (3) occurs.
3.14. Updating the Memory Cell Pool
Step (6) entails choosing the ARB member with the maximum stimulation rate (i.e., the memory cell applicant: mc_cand) from the class of antigens. Furthermore, if the activation is found to be higher compared to that of the formerly acknowledged storage cell (mc_match) to the antigen, the proposed algorithm includes mc_cand to the storage cell.
However, the identification between mc_cand and mc_match is found to be less than a user-defined threshold value of “replacement threshold” (γ), then the mc_match value is replaced by mc_cand.
By repeating the process for all antigens, a final memory cell pool will be produced. This pool may be indicated and embodied for a place distribution of the training trial collection and can be suitably used to classify new samples (antigens). Further reading on this entire process is available in [31][28].
4. Proposed Fuzzy labeling for tuberculosis diagnosis detection
For large data collection, learning methods can be very cumbersome since each sample is prepared while classifying new data, something that requires longer classification instances. This does not seem to be a problem for certain request areas, but when it comes to a subject like medical diagnosis, time is essential in addition to classification precision.
Effort has been made to improve detection accuracy by using a fuzzy system [32]. The fuzzy system adapts to the dataset to perform training labeling. This data labeling stage is realized by utilizing an AIS algorithm. This mechanism has been used to design the data reduction algorithm for our purpose.
The fuzzy AIRS is a fuzzy-based AIRS strategy for tuberculosis diagnosis detection. In designing the anomaly-based fuzzy AIRS, the Fuzzy Logic Controller was applied, which converts the continuous inputs into fuzzy sets. Ten features of tuberculosis diagnosis have been defined for the fuzzy input. This adds more dynamic behaviour to the system and enables early tuberculosis diagnosis.
The FLC inputs, denoted by complaints of cough, chest pain, leukocyte white blood cells (WBC), weight loss, night sweats, fever, shortness of breath, HIV, PPD, CD4, haemoglobin concentration (HBC), platelet count, neutrophil count (NC), lymphocyte count, erythrocyte sedimentation rate (ESR), alanine aminotransferase (ALT) level, alkaline phosphatase (ALP) level, lactate dehydrogenase (LDH) concentration, and albumin [7] concentration, correspond to the fuzzy state of the network in Eq (1).
The FLC output, given by the abnormality, represents the action of the agent, A(t). The linguistic variables (Haemoglobin, Platelet, WBC, Neutrophil, Lymphocyte, and Erythrocyte) act as inputs and the status acts as output; these are used in the experiments listed in Table 2. A small number of rules as shown in Table 3 speed up the convergence of the AIRS algorithm since fewer states must be visited during the exploration phase.
The valuation range of these fuzzy states adopts the fuzzy membership function to represent a Q-learning function. Table 3 displays some of the rules applied for Fuzzy AIRS.
(1)
Fuzzy States proposed by the rules.
| Number of states | Status of detection | Leukocytes (WBC) | Haemoglobin | Platelet | Neutrophil | Lymphocyte | Erythrocyte | Alanine | Alkaline | Lactate | Albumin |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ∂1 | Goal = Bad | Low | Low | Low | Medium | Medium | High | Low | Medium | High | Low |
| ∂2 | Goal = Bad | Medium | Low | High | Low | Medium | Low | Medium | High | Low | High |
| ∂3 | Normal = Average | High | Medium | Low | High | High | Medium | High | Low | Medium | Medium |
| ∂4 | Goal =Bad | Medium | High | Med | Low | Low | Low | High | High | Low | High |
| ∂5 | Goal =Bad | High | Low | High | Medium | High | Medium | Low | Low | Medium | Low |
| ∂6 | Normal = Average | Medium | Medium | Med | Medium | High | Low | Medium | Medium | High | Medium |
| ∂7 | Normal = Good | Medium | Medium | High | Medium | Medium | High | Medium | Medium | Medium | Medium |
| ∂8 | Normal = Average | Low | Medium | Low | Medium | Medium | Medium | Low | Low | Medium | Medium |
| ∂9 | Goal = Bad | High | High | Med | Low | Low | Medium | Medium | High | High | High |
| ∂10 | Normal = Good | Medium | High | Med | High | Medium | Medium | Medium | Medium | Medium | Medium |
The fuzzy rules.
| if (Leucocyte=Low AND Hemoglobin=Low AND Platelet=Low AND Neutrophil=Medium AND Lymphocyte=Medium AND Erythrocyte=High AND Alanine=Low AND Alkaline=Medium AND Lactate=High AND Albumin=Low) Then (status=Bad) |
|---|
| if (Leucocyte=Medium AND Hemoglobin=Low AND Platelet=High AND Neutrophil=Low AND Lymphocyte=Medium AND Erythrocyte=Low AND Alanine=Medium AND Alkaline=High AND Lactate=Low AND Albumin=High) Then (status=Bad) |
| if (Leucocyte=Medium && Hemoglobin=Medium && Platelet=Medium && Neutrophil=Medium && Lymphocyte=High && Erythrocyte=Low && Alanine=Medium && Alkaline=Medium && Lactate=High && Albumin=Medium) Then (status=Average) |
| if (Leucocyte=Medium && Hemoglobin=Medium && Platelet=High && Neutrophil=Medium && Lymphocyte=Medium && Erythrocyte=High && Alanine=Medium && Alkaline=Medium && Lactate=Medium && Albumin=Medium) Then (status=Good) |
| if (Leucocyte=Medium AND Hemoglobin=High AND Platelet=Medium AND Neutrophil=High AND Lymphocyte=Medium AND Erythrocyte=Medium AND Alanine=Medium AND Alkaline=Medium AND Lactate=Medium AND Albumin=Medium) Then (status=Good) |
5. Measures for performance evaluation
5.1. Classification accuracy, specificity and sensitivity
In this study, dataset classification accuracy was measured according to [33] Eqs. (4) and (5).
(4)
(5)
where the T has been defined as the test set (items to be classified), t0T, t.c is the category of the item t, and the function classify (t) returns the classification of t according to AIRS. For having more accurate results alongside classification accuracy, sensitivity and specificity measures are considered in Eq. (6) and (7).
(6)
(7)
where TP, TN, FP and FN denote true positives, true negatives, false positives and false negatives, respectively.
5.2. k-Fold cross validation
K-fold cross validation renders test results more valuable and popular amongst researchers. In this validation, the bias associated with the random sampling of the training [10] is minimized. All data is divided into k mutually exclusive subsets of approximately equal size. Training and testing the classification algorithm is repeated up to k times. For each case, one of the folds is selected as test data and the remaining fields are summed to form training data. In this way, k different test results can be obtained for each training-test configuration. The algorithm's test accuracy can be computed by calculating the average of these results. [10]. In our application, this system was applied as 10-fold mix validation.
5.3. Current experiment parameters
At FLC-AIS algorithm, the majority of classifier's elements are self-determined [34]. This phenomenon can decrease the efforts for discovering applicable settings for the classifier. Therefore, the following parameters of Table 4 in the present experiments very slightly effect the system's performance.
Parameters used in FQ-AIS for the tuberculosis disease dataset.
| Parameters used | Tuberculosis disease dataset |
|---|---|
| Mutation rate | 0.1 |
| ATS (affinity threshold scalar) | 0.2 |
| Stimulation threshold | 0.99 |
| Clonal rate | 10 |
| Hyper clonal rate | 2 |
| Iteration number | 500 |
| Number of resources in learning-AIRS | 175 |
6. Experimental results
With respect to proposed system applications, a Tuberculosis disease dataset was classified. The obtained research classification exhibited accuracy of 99.14%, sensitivity of 87.00%, and specificity of 86.12%. Giving these results, the maximum classification accuracy was reached with the learning rate of 0.8 (α) values. The results have been acquired by 10-fold cross validation scheme which included sensitivity and specificity values beside the classification accuracies are shown in Table 5.
Obtained efficiency parameters for highest classification precision.
| Accuracy (%) | Sensitivity (%) | Specificity (%) | 10-Fold cross validation (%) |
|---|---|---|---|
| 99.14 | 100 | 99.56 | 89 |
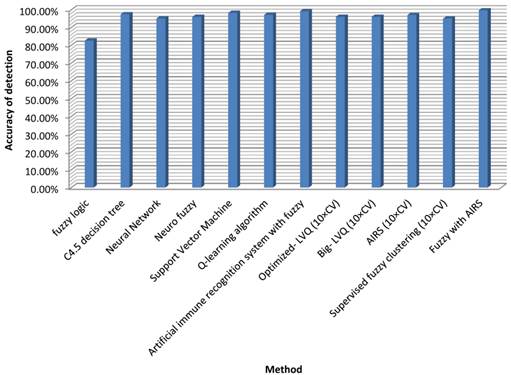
The classification accuracy attained by Fuzzy-centered AIS for TB is the highest of the classifiers noted in literature. A contrast between our method and these classifiers regarding classification precision is shown in Table 6.
Classification accuracies achieved by the research's method and other methods from the literature.
| Author (Year) | Method | Classification accuracy (%) |
|---|---|---|
| Philips et al. [13] | Fuzzy logic | 82.6 |
| Porcel et al. [14] | C4.5 decision tree | 97.45 |
| Er et al. [9] | Neural Network | 95.08 |
| Ansari et al.[15] | Neuro fuzzy | 96 |
| Chang et al.[16] | Support Vector Machine | 98.2 |
| Zhao et al.[35] | Q-learning algorithm | 97.1 |
| Polat et al. [21] | Artificial immune recognition system with fuzzy | 99.15 |
| Goodman et al. [36] | Optimized- LVQ (10×CV) | 96.7 |
| Goodman et al. [37] | Big- LVQ (10×CV) | 96.8 |
| Goodman et al. [36] | AIRS (10×CV) | 97.2 |
| Abonyi and Szeifert [38] | Supervised fuzzy clustering (10×CV) | 95.57 |
| Our proposed method | Fuzzy with AIRS | 99.70 |
Our recommended technique reached the highest classification accuracy among the classifiers in Table 6. However, the classification stability is 99.15% and an increase of 0.55% has been reached which may not be minimal for such medical problems. If more data were employed in the training phase, the effect would certainly be much more promising, or even 100%. Then the device could be used confidently to help authorities make choices in examination matters. Figure 1 illustrates the accuracy of the proposed method compared with other approaches.
7. Discussion and conclusion
The significant effects of developments and novelties in Machine Learning tools and expert system methodologies have been widely used in different domains, one of the most important fields being medicine. Based on experience from previous studies, decision making in the medical field has not been simple. The classification systems implemented in medical decision making deliver medical data for faster, more detailed inspection. Analysis of global statistical data on tuberculosis indicates that this disease is amongst the most predominant kinds.
In this research a new machine learning method of diagnosing tuberculosis has been proposed. The method is a combination between fuzzy and a data reduction phase, developed as AIS. Furthermore, a fuzzy-weighting procedure has been employed prior to this data decrease algorithm. The dataset collected from the Pasteur Institute of Northern Iran was applied in this research, making it possible to compare the proposed classification accuracy with other methods.
In the current work, 99.70% classification precision was attained via 10-fold cross validation. This is undeniably the highest accuracy rate for TB diagnosis. In addition, it was proved in this research that the proposed system can be implemented for any TB diagnosis and the classification accuracy will remain high, especially for large data sets. It is safe to say this method can be conducted in many different medical applications.
Detection accuracy for fuzzy AIRS
Acknowledgements
This paper is financially supported by the Malaysian Ministry of Education under the University of Malaya High Impact Research Grant -UM.C/HIR/625/1/MOE/FCSIT/03. This paper is also supported by Department of Health Services Administration, Science and Research Branch, Islamic Azad University, Shiraz Fars, Iran.
Competing Interests
The authors have declared that no competing interest exists.
References
1. Bird L. Infectious disease: The tuberculosis signature. Nature Reviews Immunology. 2010;10:677-677
2. Chiang CY, Van Weezenbeek C, Mori T, Enarson DA. Challenges to the global control of tuberculosis. Respirology. 2013;18(4):596-604
3. Lienhardt C. et al. Global tuberculosis control: lessons learnt and future prospects. Nature Reviews Microbiology. 2010;10:407-416
4. Phillips M, Basa-Dalay V, Bothamley G, Cataneo RN, Lam PK, Natividad MPR, Schmitt P, Wai J. Breath biomarkers of active pulmonary tuberculosis. Tuberculosis. 2010;90:145-151
5. Siddiqi K, Lambert ML, Walley J. Clinical diagnosis of smear-negative pulmonary tuberculosis in low-income countries: the current evidence. The Lancet Infectious Diseases. 2003;3:288-296
6. Programme GT. Global Tuberculosis Control: WHO Report. WHO. 2008
7. Jacobsen M, Repsilber D, Gutschmidt A, Neher A, Feldmann K, Mollenkopf H, Ziegler A, Kaufmann SE. Candidate biomarkers for discrimination between infection and disease caused by Mycobacterium tuberculosis. J Mol Med. 2007;85:613-621
8. Yoon S, MacGregor JF. Fault diagnosis with multivariate statistical models part I: using steady state fault signatures. Journal of Process Control. 2001;11:387-400
9. Er O. et al. Tuberculosis Disease Diagnosis Using Artificial Neural Networks. J Med Syst. 2010;34:299-302
10. Er O, Yumusak N, Temurtas F. Chest diseases diagnosis using artificial neural networks. Expert Systems with Applications. 2010;37:7648-7655
11. Dai Q, Liu N. Alleviating the problem of local minima in Backpropagation through competitive learning. Neurocomputing. 2012;94:152-158
12. Burse K, Manoria M, Kirar V. Improved Back Propagation Algorithm to Avoid Local Minima in Multiplicative Neuron Model. In: (ed.) Das V. et al. Information Technology and Mobile Communication. Heidelberg: Springer Berlin. 2011:67-73
13. Phillips M, Cataneo RN. Condos R, Ring Erickson GA, Greenberg J, La Bombardi V, Munawar MI, Tietje O, Volatile biomarkers of pulmonary tuberculosis in the breath. Tuberculosis. 2007;87:44-52
14. Porcel JM, Alemán C, Bielsa S, Sarrapio JT. Fernández de Sevilla, Esquerda A, A decision tree for differentiating tuberculous from malignant pleural effusions. Respiratory Medicine. 2008;102:1159-1164
15. Ansari AQ, Gupta NK, Ekata E. Adaptive neurofuzzy system for tuberculosis. 2nd IEEE International Conference on Parallel Distributed and Grid Computing (PDGC). 2012:568-573
16. Chang J, Arbeláez P, Switz N, Reber C, Tapley A, Davis JL, Cattamanchi A, Fletcher D, Malik J. Automated Tuberculosis Diagnosis Using Fluorescence Images from a Mobile Microscope. In: (ed.) Ayache N. et al. Medical Image Computing and Computer-Assisted Intervention - MICCAI 2012. Springer Berlin Heidelberg. 2012:345-352
17. Keller T, Bitterlich N, Hilfenhaus S, Bigl H, Löser T, Leonhardt P. Tumour markers in the diagnosis of bronchial carcinoma: new options using fuzzy logic-based tumour marker profiles. J Cancer Res Clin Oncol. 1998;124:565-574
18. Wang QZ, Wang K, Wang XZ, Hou Al, Li Y, Wang B. 3D Matrix Pattern Based Support Vector Machines for Identifying Pulmonary Cancer in CT Scanned Images. J Med Syst. 2012;36:1223-1228
19. Floreano D, Mattiussi C. Bio-Inspired Artificial Intelligence: Theories, Methods, and Technologies. The MIT Press. 2008
20. Dasgupta D, Yu S, Nino F. Recent Advances in Artificial Immune Systems: Models and Applications. Applied Soft Computing. 2011;11:1574-1587
21. Polat K, Güneş S. Artificial immune recognition system with fuzzy resource allocation mechanism classifier, principal component analysis and FFT method based new hybrid automated identification system for classification of EEG signals. Expert Systems with Applications. 2008;34:2039-2048
22. Polat K, Şahan S, Güneş S. Automatic detection of heart disease using an artificial immune recognition system (AIRS) with fuzzy resource allocation mechanism and k-nn (nearest neighbour) based weighting preprocessing. Expert Systems with Applications. 2007;32:625-631
23. Bianca C, Chiacchio F, Pappalardo F, Pennisi M. Mathematical modeling of the immune system recognition to mammary carcinoma antigen. BMC bioinformatics. 2012;13:S21
24. Bianca C, Pennisi M. The triplex vaccine effects in mammary carcinoma: A nonlinear model in tune with SimTriplex. Nonlinear Analysis: Real World Applications. 2012;13:1913-1940
25. Bianca C, Delitala M. On the modelling of genetic mutations and immune system competition. Computers & Mathematics with Applications. 2011;61:2362-2375
26. Castro LND, Timmis JI. Artificial immune systems as a novel soft computing paradigm. Soft Computing. 2003;7:526-544
27. Kodaz H. et al. Medical application of information gain based artificial immune recognition system (AIRS): Diagnosis of thyroid disease. Expert Systems with Applications. 2009;36:3086-3092
28. Zhao W, Davis CE. A modified artificial immune system based pattern recognition approach—An application to clinical diagnostics. Artificial Intelligence in Medicine. 2011;52:1-9
29. Polat K, Güneş S, Tosun S. Corrigendum to “Diagnosis of heart disease using artificial immune recognition system and fuzzy weighted pre-processing”[Pattern Recognition 39 (11)(2006) 2186-2193]. Pattern Recognition. 2011;44:1327
30. Er O, Yumusak N, Temurtas F. Diagnosis of chest diseases using artificial immune system. Expert Systems with Applications. 2012;39:1862-1868
31. Watkins A, Boggess L. A new classifier based on resource limited artificial immune systems. Proceedings of the 2002 Congress on Evolutionary Computation. 2002:1546-1551
32. Shamshirband S, Kalantari S, Bakhshandeh Z. Designing a smart mul-ti-agent system based on fuzzy logic to improve the gas consumption pattern. Scientific Research and Essays. 2010;5:592-605
33. Watkins AB. AIRS: A resource limited artificial immune classifier. Mississippi State University. 2001
34. Fayyad U, Piatetsky-Shapiro G, Smyth P, Uthurusamy R. Advances in Knowledge Discovery and Data Mining. The MIT Press. 1996
35. Zhao Y, Zeng D, Socinski MA, Kosorok MR. Reinforcement Learning Strategies for Clinical Trials in Nonsmall Cell Lung Cancer. Biometrics. 2011;67:1422-1433
36. Goodman DE, Boggess L, Watkins A. Artificial immune system classification of multiple-class problems. Proceedings of the artificial neural networks in engineering ANNIE. 2002;2:179-183
37. DE Goodman J, Boggess L, Watkins A. An investigation into the source of power for AIRS, an artificial immune classification system. Proceedings of the International Joint Conference on Neural Networks. 2003:1678-1683
38. Abonyi J, Szeifert F. Supervised fuzzy clustering for the identification of fuzzy classifiers. Pattern Recognition Letters. 2003;24:2195-2207
Author contact
![]() Corresponding author: Shahaboddin Shamshirband E-mail: shahab1396com.
Corresponding author: Shahaboddin Shamshirband E-mail: shahab1396com.

 Global reach, higher impact
Global reach, higher impact