PDF

Int J Med Sci 2018; 15(1):16-22. doi:10.7150/ijms.20522 This issue Cite

Research Paper

Optimal Load for Bone Tissue Scaffolds with an Assigned Geometry

Antonio Boccaccio¹ , Antonio E. Uva¹, Michele Fiorentino¹, Giuseppe Monno¹, Andrea Ballini², Apollonia Desiate³

1. Department of Mechanics, Mathematics and Management, Politecnico di Bari, Bari 70126, Italy;
2. Department of Base Medical Sciences, Neurosciences and Sense Organs, University of Bari “Aldo Moro”, Bari, Italy;
3. Interdisciplinary Department of Medicine, Section of Dentistry, School of Medicine, University of Bari “Aldo Moro”, Bari, Italy;

✉ Corresponding author: Dr. Antonio Boccaccio, Mailing Address: Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari, Viale Japigia, 182, I-70126, Bari, Italy Contact Information: Tel: +39-0805962705 Fax: +39-0805962777 E-mail: a.boccaccioit or antonio.boccaccioit More

Abstract

Thanks to the recent advances of three-dimensional printing technologies the design and the fabrication of a large variety of scaffold geometries was made possible. The surgeon has the availability of a wide number of scaffold micro-architectures thus needing adequate guidelines for the choice of the best one to be implanted in a patient-specific anatomic region. We propose a mechanobiology-based optimization algorithm capable of determining, for bone tissue scaffolds with an assigned geometry, the optimal value L_opt of the compression load to which they should be subjected, i.e. the load value for which the formation of the largest amounts of bone is favoured and hence the successful outcome of the scaffold implantation procedure is guaranteed. Scaffolds based on hexahedron unit cells were investigated including pores differently dimensioned and with different shapes such as elliptic or rectangular. The algorithm predicted decreasing values of the optimal load for scaffolds with pores with increasing dimensions. The optimal values predicted for the scaffolds with elliptic pores were found higher than those with rectangular ones. The proposed algorithm can be utilized to properly guide the surgeon in the choice of the best scaffold type/geometry that better satisfies the specific patient requirements.

Keywords: Scaffolds for Bone Tissue Engineering, Computational Mechanobiology, Numerical Optimization Algorithms, Hexahedron Unit Cell, Printing of Biomaterials.

Introduction

Scaffolds for bone tissue engineering are porous biomaterials that imitate the structure and the properties of natural bone and that are implanted into anatomic regions where large volumes of bone - due to different reasons such as cleft palate, trauma, primary tumor resections or selective surgery - are missing. Scaffolds must be properly shaped and designed so as to correctly bear the load acting on them as well as to promote and favor all the biological processes involved in the bone formation process such as vascularization [1], signaling, production of extra-cellular matrix [2] and delivering of biofactors [3,4].

Biomaterials science traditionally adopts a 'trial-and-error' approach, with changes made on an existing design, based on in vitro or in vivo experimental findings. However, in vitro or in vivo experimentation requires costly protocols and procedures very expensive in terms of time [5]. Furthermore, it was found that the osteogenesis process occurring in vivo does not always match the same process reproduced in vitro. For instance, Karageorgiou and Kaplan [6] showed that a lower porosity stimulates osteogenesis in vitro while a higher porosity leads to the formation of larger amounts of bone in vivo. This discrepancy pushed a large number of researchers to develop in silico (computational) models that allow to simulate the effects of environment on the mechanobiological stimuli and, hence, to predict how this environment affects the tissue differentiation process [7-9].

A very large number of factors must be taken into account to properly design bony tissue scaffolds, including the variability of bone tissue properties, the differences in sex, age, activity and disease status of individuals [3,10,11]. In order to optimize the healing process and hence to shorten its duration, customized solutions of scaffolds ad hoc designed for patient-specific anatomic regions should be adopted [12]. Nowadays, this was made possible especially thanks to the recent advances in three-dimensional (3D) printing technologies that allow to fabricate practically any type of scaffolds with any arbitrarily complex geometry [13-15]. The impressive potential offered by these technologies is to provide highly complex constructs with patient-specific designs as well as rapid on-demand fabrication at a low cost [16]. The possibility of designing and producing scaffolds with any arbitrary geometry, led many researchers to investigate different scaffold microstructure geometries based on different unit cells such as: cubic, rhombic dodecahedron, pyramidal, rhombicuboctahedron and diamond [17-23]. The wide gamma of scaffold geometries currently available makes mandatory to give guidelines to the surgeon (e.g. dental, maxillofacial, oral, orthopaedic, etc) in the choice of the best scaffold micro-architecture that is the most suited to the specific patient requirements. In other words, having at h(er)is disposal a large number of scaffold geometries, the surgeon needs to be properly guided to identify the best one that allows the scaffold performances to be maximized and hence the successful outcome of the scaffold implantation to be guaranteed. In this paper we present an algorithm based on mechanobiological principles that, known the geometry of the scaffold is capable of giving in output the optimal load L_opt with which 'that' scaffold should be loaded to obtain the best scaffold performance. A practical approach that can be adopted is the following. The algorithm can be first implemented to determine the optimal load value for a large number of scaffold geometries. Then, based on the anthropometric features of the specific patient and implementing multi-scale approaches - such as, for example, the approach utilized in a previous study [24] -, possible values of load L_patient acting on a generic scaffold implanted into 'that' patient-specific anatomic region can be hypothesized. Therefore, the surgeon will select/choose, - among the scaffolds for which the optimal load was determined via the proposed algorithm, - the scaffold with L_opt as close as possible to L_patient.

Materials and Methods

The scaffold models investigated

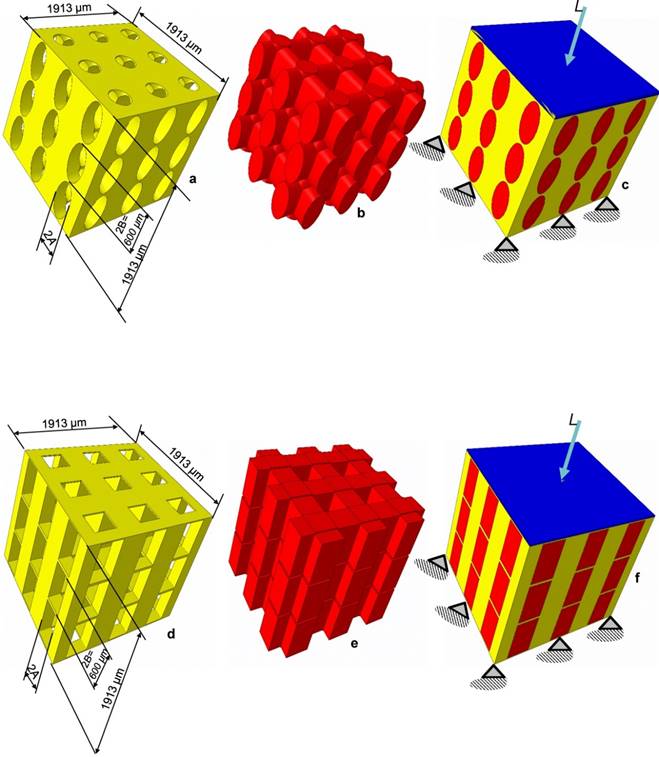
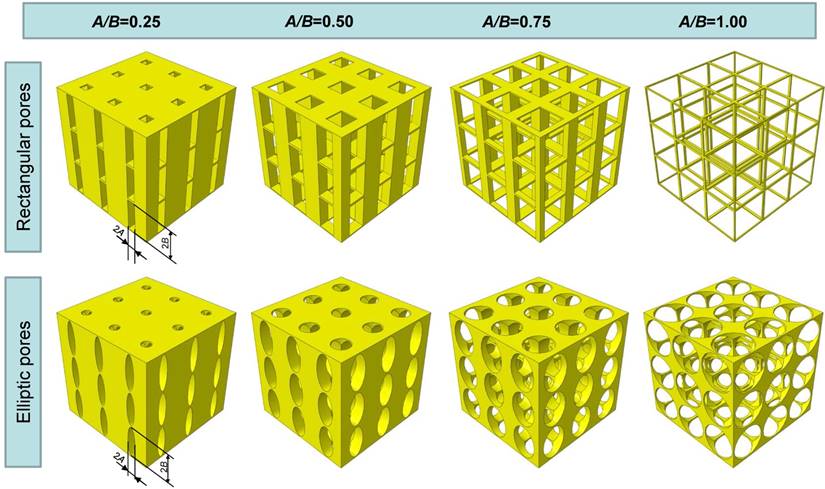
Two different models of scaffold were investigated in this study: a scaffold including elliptic pores (Figure 1a) and a scaffold including rectangular ones (Figure 1d). The principal scaffold dimensions, which are consistent with those utilized in previous studies [12, 25], are shown in Figure 1. Each pore (elliptic or rectangular) was hypothesized to have the height 2B of 600 µm, while four different values were given to the width 2A which correspond to have the following values of the ratio A/B: 0.25, 0.5, 0.75 and 1.00 (Figure 2).

Each model included the scaffold (represented in yellow, Figures 1a and 1d), the mesenchymal tissue (represented in red, Figures 1b and 1e) which occupies the scaffold pores and a rigid plate (represented in blue, Figures 1c and 1f) through which a compression load L (Figure 1) was applied on the model upper surface. These models were discretized into finite elements and given in input to a finite element code (ABAQUS, Version 6.12, Dassault Systèmes, France). The bottom surface of the model was clamped with 'encastre' boundary conditions. Both, the scaffold and the mesenchymal tissue were modelled as poroelastic materials. The scaffold Young's modulus was set equal to 1000 MPa while the mechanical properties implemented for the other materials are the same as those utilized in previous studies [12,25].

The algorithm for the determination of the optimal load

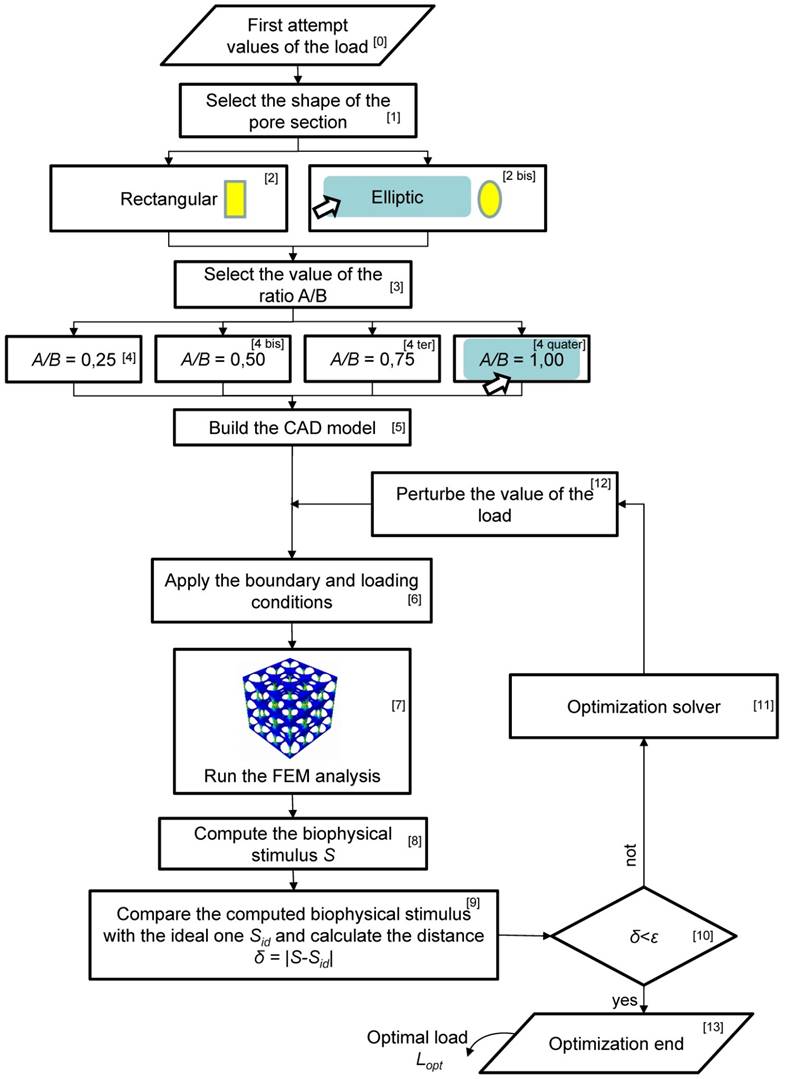
An ad hoc algorithm, a schematic of which is depicted in Figure 3, was written in MATLAB® (Version R2016b) environment to determine the optimal load for each of the scaffold geometries investigated in this study. The algorithm requires, first of all, to fix a first attempt value for the optimal load (Block [0]). In detail, the algorithm requires to set the value of the load per unit area (units, N/mm²), i.e. the value of the pressure exerted by the rigid plate on the upper model surface (Figure 1). After selecting the shape of the pore (Block [1], Block [2] and Block [2bis], Figure 3), the user is asked to set the value of the ratio A/B (Block [3], Block [4], Block [4bis], Block [4ter], Block [4quater], Figure 3). For example, in Figure 3 the case where the elliptic pore and the value A/B = 1.00 are selected, is shown. Then, the CAD model of the scaffold with the selected pore shape and ratio A/B is built, discretized into finite elements and given in input to the finite element solver (Block [5]). On this model, the boundary and loading conditions described above are applied (Block [6]) and a finite element analysis is run (Block [7]). Based on the values of the stress and strain predicted by the finite element analysis, the algorithm computes a biophysical stimulus S that depends on the octahedral shear strain and the interstitial fluid flow. Further details on this quantity as well as on the methodology adopted to compute it are reported in previous studies [12,24]. Then, the algorithm compares the computed biophysical stimulus with the ideal one S_id, i.e. the biophysical stimulus that corresponds to have all the scaffold pores occupied entirely by mature bone. If the distance/difference δ = |S-S_id| is smaller than an a priori fixed small quantity ε (Block [10]), then the algorithm stops and gives in output the optimal compression load L_opt (for the specific scaffold geometry investigated). If, instead the distance/difference δ is greater than ε, then the algorithm starts a new optimization cycle (Block [11]), perturbs the value of load initially fixed (Block [12]) and applies this new load on the finite element model (Block [6]). A new finite element analysis is performed (Block [7]) that will give new levels of stress and strain and hence a new value of the biophysical stimulus S (Block [8]). At this point, the algorithm will perform so many optimization cycles until the inequality δ = |S-S_id| < ε is satisfied. Once this occurs, the algorithm stops and gives in output the optimal value of load L_opt. In other words, the algorithm perturbs the value of the load acting on the scaffold until the volume of the mesenchymal tissue experiencing a biophysical stimulus S ≈ S_id is maximized.

 Figure 1 

CAD model of the scaffold (a,d), the mesenchymal tissue occupying the pores (b,e) and of the system scaffold/tissue (c,f). Scaffolds based on the hexahedron unit cell and with elliptic (a-c) and rectangular (d-f) pores were studied. The lower base of model was clamped while a compression load L was applied on the upper surface via a rigid plate (highlighted in blue) (c,f). The principal dimensions of the models investigated in the study are shown.

 Figure 2 

Scaffold geometrical configurations investigated in the study. Scaffolds with elliptic and rectangular pores were considered with different values of the ratio A/B.

The algorithm described above can be properly utilized to guide the surgeon in the choice of the most suitable scaffold to be implanted in a patient-specific anatomic region. To do this, the following procedure can be adopted. The algorithm should be first implemented to determine the optimal load L_opt for all the scaffold geometries that the surgeon has at h(er)is disposal. Then, based on the anthropometric features of the patient and adopting multi-scale approaches [24], a possible value of the load L_patient acting in a generic scaffold implanted into the anatomic region of 'that' patient can be hypothesized. In detail, the multi-scale approach requires to build a micro-scale and a macro-scale models. The macro-scale model represents the model of the anatomic region where the scaffold will be implanted, while the micro-scale model represents the model of the scaffold to be implanted. These two models exchange information with each other: in particular, localization rules allow passing from the macro- to the micro-scale model, vice-versa, homogenization rules allow passing from micro- to macro-scale model. Based on the anthropometric information of the patient, the macro-scale model can be easily generated. Then, through localization rules the loading conditions L_patient acting on the micro-scale model (i.e. the scaffold) can be computed. The value of load deriving from the localization rule can then be compared with the optimal load L_opt determined via the proposed algorithm. The surgeon will choose the scaffold with the value of L_opt as close as possible to L_patient.

All the optimization analyses were performed on a HP XW6600- Intel® Xeon® Dual-Processor E5-5450 3 GHz - 32 Gb RAM and took some 360 hours of computation.

Results and Discussion

Increasing levels of the ratio A/B lead to decreasing values of the predicted optimal load (Figure 4) (predicted values of the optimal load are expressed as load per unit area, units N/mm²). This is consistent with our expectations. In fact, as A/B decreases, the global stiffness of the scaffold decreases too and with it the optimal load the scaffold is capable to bear. Interestingly, it appears that for fixed levels of the ratio A/B, the optimal load predicted for scaffolds with elliptic pores is higher than that predicted for scaffolds with rectangular ones. Also this result is consistent with our expectations as for given values of A/B, scaffolds with elliptic pores include more material and hence are stiffer than those with rectangular pores (please, see Figure 2 that shows the geometrical configurations of scaffolds for different levels of A/B and for the different pore shapes investigated in this study).

 Figure 3 

Schematic of the flow-chart implemented in the study to determine the optimal load acting on the scaffold

 Figure 4 

Optimal load (expressed as load per unit area, [N/mm²]) predicted by the optimization algorithm for the different scaffold geometries investigated in the study. The diagram can be properly utilized to choose the best scaffold geometry that is better suited for the specific patient requirements. Let us suppose, for example, that a value of L_patient = 0,35 MPa was found. It appears that the best scaffold geometry that can be selected by the surgeon is the one with rectangular pores and a ratio A/B = 0,5. The second best solution is a scaffold with elliptic pores and with A/B = 0,75.

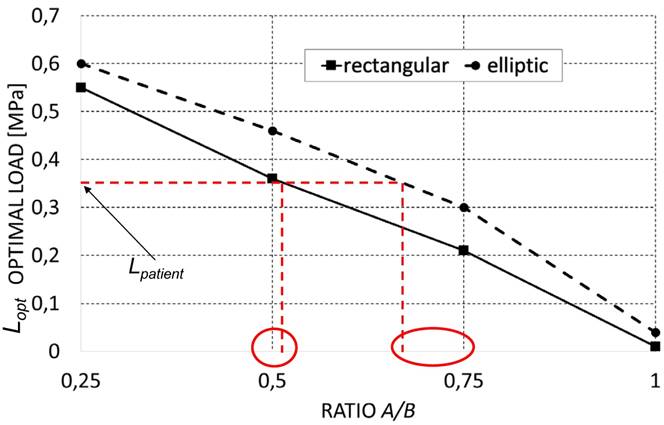
The diagram can be properly utilized to choose the best scaffold geometry that is better suited for the specific patient requirements. Let us suppose, for example, that a value of L_patient = 0,35 MPa was found (Figure 4). It appears that the best scaffold geometry that can be selected by the surgeon is the one with rectangular pores and a ratio A/B = 0.5. The second best solution is a scaffold with elliptic pores and with A/B = 0.75.

The present study has some limitations. First, scaffold models with small dimensions have been considered. In general, scaffolds implanted in the human body can have larger dimensions than those hypothesized. The strategy of considering rather small models was adopted to decrease the computational cost of the optimization analyses which are very expensive in terms of computational time. Furthermore, in the present article we intend just to demonstrate the feasibility of the proposed approach. Increases in computational power will ultimately allow more realistic models to be developed. Second, the optimal load was investigated by considering the value of a biophysical stimulus S that does not depend on the other factors that can affect the bone regeneration process such as: angiogenesis [26], scaffold dissolution [27], growth factors [28] (e.g. platelet-rich fibrin (PRF) [29] and platelet-rich plasma (PRP) [30]). Neglecting the angiogenesis, the proposed model was not capable of taking into account other possible aspects that are strictly related to the vascular networks such as the effects of smoking [31]. Moreover, other systemic conditions have not been considered such as the oxidative stress balance which certainly affects the healing process [32]. We expect that both, the oxidative stress as well as the use of growth factors biomatrix will lead to altered values of the ideal stimulus S_id and hence to altered values of the optimal load L_opt. Further investigations should be carried out on these topics in the future. However, previous studies [12,25] that neglected such factors and adopted the same definition of the biophysical stimulus S - utilised in the present study -, were capable of successfully predicting the optimal scaffold geometry.

In spite of the above mentioned limitations, the proposed algorithm predicts values of the optimal load that are consistent with those reported in other studies [27]. Furthermore, the trend of the predicted optimal load is consistent with the physics of the problem. The predicted optimal loads are also in agreement with those reported in previous studies [12,25] where patterns of bony tissues consistent with those observed in vitro were predicted. Future studies should implement computational mechanobiological models on other possible scaffold types such as hydrogel scaffolds derived from bone extracellular matrix, scaffolds seeded on collagen I [33] and biomimetic scaffolds [10].

Conclusions

A mechanobiology-based algorithm was developed capable of predicting, for scaffolds with assigned geometry, the optimal load, i.e. the load level that favours the formation of the largest amounts of bone. The algorithm predicted the optimal load of scaffolds with hexahedron unit cells including elliptic and rectangular pores. For a fixed scaffold geometry, the algorithm compares the biophysical stimulus S actually acting on the mesenchymal tissue and an ideal value S_id which corresponds to have all the scaffold pores occupied entirely by mature bone. The algorithm perturbs so many times the value of load acting on the scaffold, until the distance/difference δ = |S-S_id| becomes smaller than an a priori fixed small quantity ε. Once this occurs, the algorithm stops and gives in output the value of the optimal load that allows the formation of bone to be maximized. It was found that for fixed levels of the ratio A/B, the optimal load predicted for scaffolds with elliptic pores is higher than that predicted for scaffolds with rectangular ones. The proposed algorithm can be utilized to guide the surgeon in the choice of the best scaffold to implant and hence to determine the scaffold geometry/type that is the most suited for the patient-specific anatomic region.

Competing Interests

The authors have declared that no competing interest exists.

References

1. Bramfeld H, Sabra G, Centis V, Vermette P. Scaffold vascularization: a challenge for three-dimensional tissue engineering. Current medicinal chemistry. 2010;17(33):3944-3967

2. Murphy CM, Haugh MG, O'Brien FJ. The effect of mean pore size on cell attachment, proliferation and migration in collagen-glycosaminoglycan scaffolds for bone tissue engineering. Biomaterials. 2010;31(3):461-466

3. Hollister SJ. Porous scaffold design for tissue engineering. Nature materials. 2005;4(7):518-524

4. Tatullo M, Marrelli M, Paduano F. The regenerative medicine in oral and maxillofacial surgery: the most important innovations in the clinical application of mesenchymal stem cells. International journal of medical sciences. 2015;12(1):72

5. Sanz-Herrera J, Garcia-Aznar J, Doblaré M. On scaffold designing for bone regeneration: a computational multiscale approach. Acta Biomaterialia. 2009;5(1):219-229

6. Karageorgiou V, Kaplan D. Porosity of 3D biomaterial scaffolds and osteogenesis. Biomaterials. 2005;26(27):5474-5491

7. Boccaccio A, Messina A, Pappalettere C, Scaraggi M. Finite element modelling of bone tissue scaffolds. Jin Z, editor. Computational Modelling of Biomechanics and Biotribology in the Musculoskeletal System: Biomaterials and Tissues. 2014:485-511

8. Sun W, Lal P. Recent development on computer aided tissue engineering—a review. Computer methods and programs in biomedicine. 2002;67(2):85-103

9. Sun W, Darling A, Starly B, Nam J. Computer-aided tissue engineering: overview, scope and challenges. Biotechnology and applied biochemistry. 2004;39(1):29-47

10. Boccaccio A, Ballini A, Pappalettere C, Tullo D, Cantore S, Desiate A. Finite element method (FEM), mechanobiology and biomimetic scaffolds in bone tissue engineering. International Journal of Biological Sciences. 2011;7(1):112-132

11. Yang S, Leong K-F, Du Z, Chua C-K. The design of scaffolds for use in tissue engineering. Part I. Traditional factors. Tissue engineering. 2001;7(6):679-689

12. Boccaccio A, Uva AE, Fiorentino M, Lamberti L, Monno G. A mechanobiology-based algorithm to optimize the microstructure geometry of bone tissue scaffolds. International Journal of Biological Sciences. 2016;12(1):1-17

13. Giannitelli S, Accoto D, Trombetta M, Rainer A. Current trends in the design of scaffolds for computer-aided tissue engineering. Acta biomaterialia. 2014;10(2):580-594

14. Lacroix D, Planell JA, Prendergast PJ. Computer-aided design and finite-element modelling of biomaterial scaffolds for bone tissue engineering. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. 2009;367(1895):1993-2009

15. Velasco MA, Narváez-Tovar CA, Garzón-Alvarado DA. Design, materials, and mechanobiology of biodegradable scaffolds for bone tissue engineering. BioMed research international. 2015:2015

16. Do A-V, Khorsand B, Geary SM, Salem AK. 3D printing of scaffolds for tissue regeneration applications. Advanced healthcare materials. 2015;4(12):1742-1762

17. Buffel B, Desplentere F, Bracke K, Verpoest I. Modelling open cell-foams based on the Weaire-Phelan unit cell with a minimal surface energy approach. International Journal of Solids and Structures. 2014;51(19):3461-3470

18. Ptochos E, Labeas G. Shear modulus determination of cuboid metallic open-lattice cellular structures by analytical, numerical and homogenisation methods. Strain. 2012;48(5):415-429

19. Ahmadi S, Campoli G, Yavari SA, Sajadi B, Wauthlé R, Schrooten J. et al. Mechanical behavior of regular open-cell porous biomaterials made of diamond lattice unit cells. Journal of the mechanical behavior of biomedical materials. 2014;34:106-115

20. Hedayati R, Sadighi M, Mohammadi-Aghdam M, Zadpoor A. Mechanical properties of regular porous biomaterials made from truncated cube repeating unit cells: Analytical solutions and computational models. Materials Science and Engineering: C. 2016;60:163-183

21. Campoli G, Borleffs M, Yavari SA, Wauthle R, Weinans H, Zadpoor AA. Mechanical properties of open-cell metallic biomaterials manufactured using additive manufacturing. Materials & Design. 2013;49:957-965

22. Hedayati R, Sadighi M, Mohammadi-Aghdam M, Zadpoor A. Mechanics of additively manufactured porous biomaterials based on the rhombicuboctahedron unit cell. Journal of the mechanical behavior of biomedical materials. 2016;53:272-294

23. Hedayati R, Sadighi M, Mohammadi Aghdam M, Zadpoor AA. Mechanical properties of additively manufactured thick honeycombs. Materials. 2016;9(8):613

24. Boccaccio A, Kelly DJ, Pappalettere C. A mechano-regulation model of fracture repair in vertebral bodies. Journal of Orthopaedic Research. 2011;29(3):433-443

25. Boccaccio A, Uva AE, Fiorentino M, Mori G, Monno G. Geometry design optimization of functionally graded scaffolds for bone tissue engineering: A mechanobiological approach. PloS one. 2016;11(1):e0146935

26. Sandino C, Checa S, Prendergast PJ, Lacroix D. Simulation of angiogenesis and cell differentiation in a CaP scaffold subjected to compressive strains using a lattice modeling approach. Biomaterials. 2010;31(8):2446-2452

27. Byrne DP, Lacroix D, Planell JA, Kelly DJ, Prendergast PJ. Simulation of tissue differentiation in a scaffold as a function of porosity, Young's modulus and dissolution rate: application of mechanobiological models in tissue engineering. Biomaterials. 2007;28(36):5544-5554

28. Bailon-Plaza A, Van Der Meulen MC. A mathematical framework to study the effects of growth factor influences on fracture healing. Journal of Theoretical Biology. 2001;212(2):191-209

29. Marrelli M, Tatullo M. Influence of PRF in the healing of bone and gingival tissues. Clinical and histological evaluations. Eur Rev Med Pharmacol Sci. 2013;17(14):1958-62

30. Wang X, Zhang Y, Choukroun J, Ghanaati S, Miron RJ. Behavior of gingival fibroblasts on titanium implant surfaces in combination with either injectable-PRF or PRP. International Journal of Molecular Sciences. 2017;18(2):331

31. Tatullo M, Gentile S, Paduano F, Santacroce L, Marrelli M. Crosstalk between oral and general health status in e-smokers. Medicine. 2016;95(49):e5589

32. Inchingolo F, Marrelli M, Annibali S, Cristalli MP, Dipalma G, Inchingolo AD. et al. Influence of endodontic treatment on systemic oxidative stress. International journal of medical sciences. 2014;11(1):1

33. Paduano F, Marrelli M, White LJ, Shakesheff KM, Tatullo M. Odontogenic differentiation of human dental pulp stem cells on hydrogel scaffolds derived from decellularized bone extracellular matrix and collagen type I. PloS one. 2016;11(2):e0148225

Author contact

Corresponding author: Dr. Antonio Boccaccio, Mailing Address: Dipartimento di Meccanica, Matematica e Management, Politecnico di Bari, Viale Japigia, 182, I-70126, Bari, Italy Contact Information: Tel: +39-0805962705 Fax: +39-0805962777 E-mail: a.boccaccioit or antonio.boccaccioit

Received 2017-4-11
Accepted 2017-7-24
Published 2018-1-1

Citation styles

©2024 Ivyspring International Publisher. Terms of use